On average a shop sells 750 kg per day with a standard deviation of 60 kilo’s. We assume sales are normal. If the shop has 850 kilograms in stock at the beginning of the day, what is the probability it runs out that day?
1 Answer
Roughly a 4.7% chance.
Explanation:
Since we are told that the sales are normal, we can use a normal distribution to answer this problem. We are given a handful of parameters to get started:
Let
If the shop was to sell out in this example, when they start the day with 850 kg, this implies that sales for the day must be at least 850 kg - obviously if the shop "sells" more than 850 kg they will owe products to customers they can't deliver!
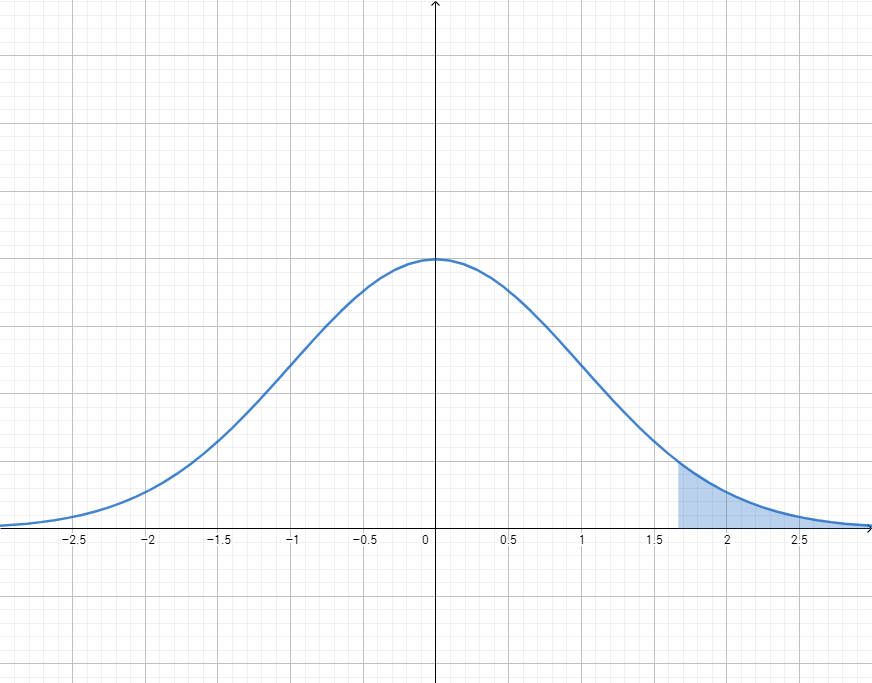
In terms of a normal distribution, this is essentially the same as asking what is the probability
To solve this, we will need to determine what the
Recall the formula for a
For
A z-score of 1.667 corresponds to a cumulative probability of about 0.953, meaning the right-tail probability is:
There is roughly a 4.7% chance the store will sell out during the day.