On the EM Spectrum, which type of wave has the most energy?
1 Answer
Gamma rays.
Explanation:
A general guideline tends to be : short wavelength, high energy . But here is a way to show which waves are the most energetic:
The energy of a wave is given by the equation:
Hence we can see that the energy of a wave is proportional to its frequency, as the other term is a constant.
Then we can ask ourselves, which waves are the ones with the highest frequency?
If we use another equation:
Then we can see that, as
Now if we use this diagram of the EM-spectrum which show wavelengths:
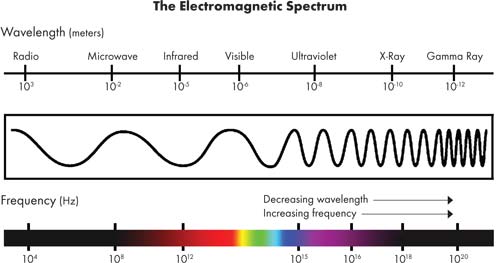 Western Reserve public media
Western Reserve public media
We can thus conclude that the waves that have the shortest wavelength are gamma rays, and thus they are the most energetic because they must also have the highest frequency.

