One mole of an ideal gas does 3000 J of work on its surroundings as it expands isothermally to a final pressure of 1.00 atm and volume of 250 L. What is the initial volume and the temperature of the gas?
1 Answer
First, let's note a few important conditions:
- Isothermal means the temperature is held constant, so
#color(green)(DeltaT = 0)# .
In these conditions, there is no change in enthalpy
- We are given final pressure but not initial pressure, and final volume but not initial volume. So, we would probably have to manipulate the Ideal Gas Law
#PV = nRT# for#T# , and maybe something to do with the work function for#V_1# .
REVERSIBLE WORK VS VOLUME
Now, we should know that reversible (efficient) work is defined as:
#\mathbf(w_"rev" = -intPdV)#
For this problem, the depiction in a PV-diagram goes like this:
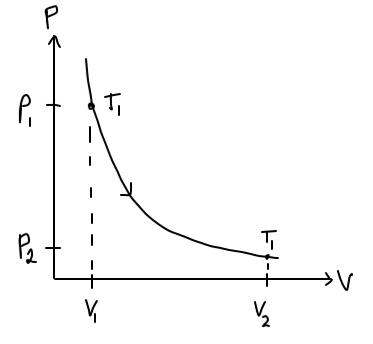
However, since we do not know
#w_"rev" = -int_(V_1)^(V_2)(nRT)/VdV#
Since
#w_"rev" = -nRTint_(V_1)^(V_2)1/VdV#
#= -nRTln|V_2/V_1|#
At this point, the shape of the PV-diagram curve looks sensible; it resembles the shape of a
THE INITIAL VOLUME FOR THE EXPANSION
We are given the work, so we should be able to solve for the initial volume,
That makes sense because
#-w_"rev"/(nRT) = ln|V_2/V_1|#
#e^(-w_"rev""/"nRT) = V_2/V_1#
#e^(w_"rev""/"nRT) = V_1/V_2#
#color(green)(V_1 = V_2e^(w_"rev""/"nRT))#
However, we do not know the temperature yet, so we'll have to put off calculating the initial volume for a bit longer.
THE TEMPERATURE FOR THE EXPANSION
Something we do know is that the temperature remained constant, so
#P_1V_1 = color(blue)(nR)T#
#color(blue)(P_2V_2) = color(blue)(nR)T#
We know the values of what is in blue, which is enough.
#color(blue)(T) = (P_2V_2)/(nR) = (("1 atm")("250 L"))/(("1 mol")("0.082057 L"cdot"atm/mol"cdot"K"))#
#=# #color(blue)("3046.66 K")#
Now we can find the initial volume:
#color(blue)(V_1) = ("250 L")e^((-"3000 J")"/"[("1 mol")("8.314472 J/mol"cdot"K")("3046.66 K")]#
#=# #color(blue)("222.08 L")#
(As an aside, if you were curious, the initial pressure was about

