One #"mol"# of an ideal gas, initially at #"300 K"#, is cooled at constant #"V"# so that #"P"_f# is #1/4 "P"_i#. Then the gas expands at constant #"P"# until it reaches #"T"_i# again. What is the work #w# done on the gas?
1 Answer
DISCLAIMER: Yes, this will be long!
This is one of those problems where drawing a "P-V diagram" would really help. Let's see approximately what that looks like for this problem.
We know that:
STEP 1
STEP 2
From that, we construct the PV-diagram as follows:
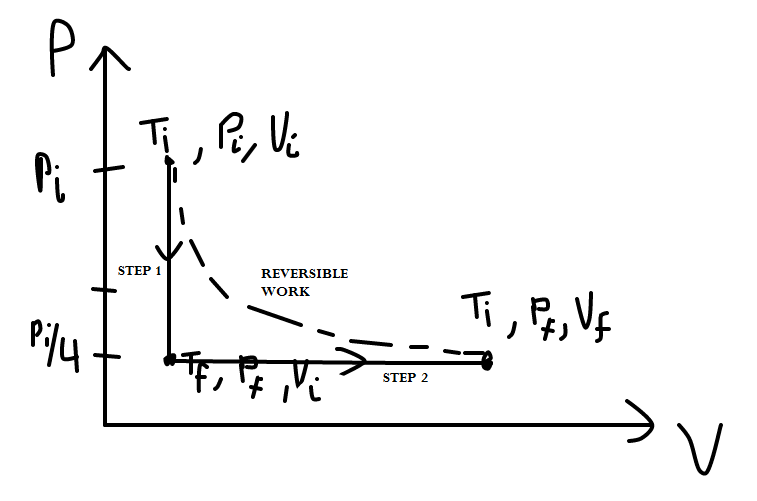
Notice how we have the possibility for a reversible work process that accomplishes the same thing more efficiently.
TWO-STEP PATH: STEP 1
We should know that inexact differential work
STEP 1: WORK
We can then proceed by noting that
#color(blue)(w_1) = - int PdV = color(blue)(0)#
STEP 1: HEAT FLOW
Since PV-work didn't happen here, it was all heat flow, conducting out through the surfaces of the container, slowly leading the gas particles to redistribute more loosely without changing in volume, thus naturally cooling the gas.
In other words, the change in internal energy was all due to heat flow at a constant volume
#color(blue)(DeltaU = q_V = ???)#
Unfortunately we don't know enough to determine
#\mathbf(DeltaU = q_V#
#\mathbf(= int_(T_1)^(T_2) C_v dT)#
Either way, this release of thermal energy means that the first work step was inefficient; thermal energy escaped the container while the work
TWO-STEP PATH: STEP 2
Okay, so what's
STEP 2: WORK
#w_2 = -int PdV#
#color(green)(w_2) = -P int_(V_i)^(V_f) dV#
#= -P(V_f - V_i)#
We don't know how the volume changed, but using the ideal gas law, we can fidget with this:
#= -cancel(P)((nRT_f)/cancel(P) - (nRT_i)/cancel(P))#
#= color(green)(-nR(T_f - T_i))#
STEP 2: TEMPERATURE
Alright, so we know
#PV = nRT#
#P_icancel(V_i)^("constant") = cancel(nR)^("constant")T_i#
#P_fcancel(V_i)^("constant") = cancel(nR)^("constant")T_f#
#P_i/T_i = P_f/T_f#
The temperature from step 1 we want is
#T_f = (P_f)/(P_i)xxT_i = 1/4 xx 300 = color(green)("75 K")#
Thus, in step 2, the gas heated from
#color(blue)(w_2 = -"1870.76 J")#
In expansion work, work is done by the gas, so it should be negative.
REVERSIBLE WORK PATH
Now, if we try that reversible path, we assume that steps 1 and 2 aren't there and that this is an efficient path where the gas is acted upon very slowly so that it has time to adjust. We know that in this path,
REVERSIBLE WORK PATH: WORK
#w_"rev" = -int PdV#
#= -int (nRT)/V dV#
#color(green)(w_"rev") = -nRT int_(V_i)^(V_f) 1/V dV#
#= color(green)(-nRTln|(V_f)/(V_i)|)#
Notice how the negative natural logarithm approximates the shape of the reversible path.
REVERSIBLE WORK PATH: VOLUME
Okay, but how did the volume change? Inversely proportionally to the pressure! The volume increased at a constant temperature, so the pressure should decrease.
Using the same trick with the ideal gas law as before:
#color(green)(w_"rev") = -nRTln|(cancel(nRT)/P_f)/(cancel(nRT)/P_i)|#
#= -nRTln|(P_i)/(P_f)|#
#= -nRTln|(P_i)/(1/4 P_i)|#
#= color(green)(-nRTln4)#
So, with
#color(blue)(w_"rev" = -"3457.89 J")#
In expansion work, work is done by the gas, so it should be negative.

