One more rectangular-shaped piece of metal siding needs to be cut to cover the exterior of a pole barn. The area of the piece is #30# #ft^2#. The length is 1 less than 3 times the width. How wide should the metal piece be?
1 Answer
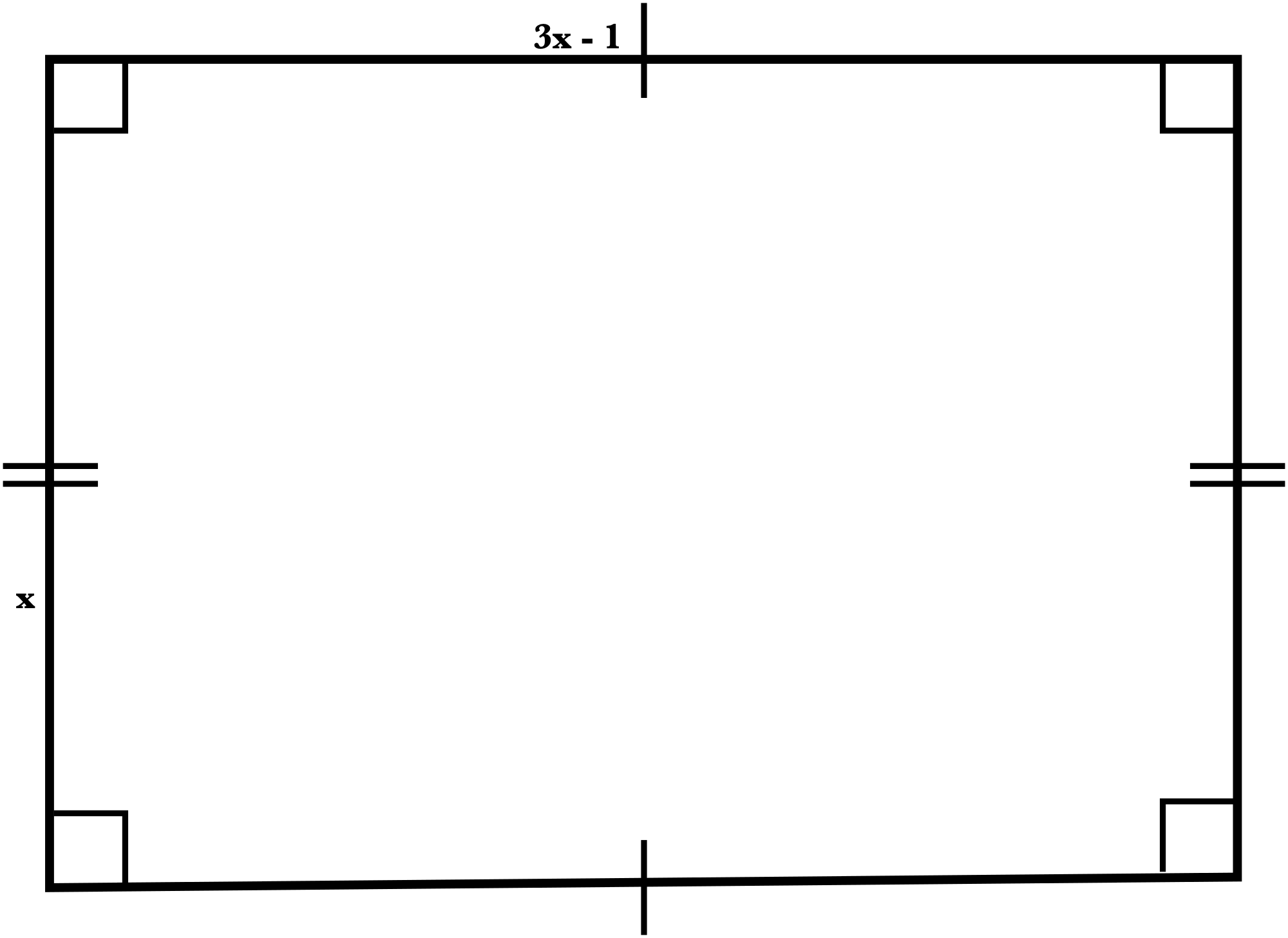
Draw a diagram to represent the situation.
Explanation:
The formula for area of a rectangle is
We know:
L = 3x - 1
W = x
A= 30
All we have to do is solve for x.
This trinomial is factorable. Since it is of the form
Since a negative side length is impossible, the width must measure
The dimensions of the piece of metal would be
Practice exercises:
-
A rectangle has an area of
#72 cm^2# . The length measures two more than four times the width. Find the perimeter of the rectangle. -
A right triangle has two legs and a hypotenuse. The hypotenuse measures
#sqrt(1000)# inches. The longer leg measures ten less than the double of the shorter leg. Find the area of the triangle. -
A rectangle has a perimeter of 46 meters. Its area is
#126 meters^2# .
Good luck!

