Payton colored a composite shape made up semicircles whose diameters are the sides of a square. The result is a shape given below. Find the area of the shaded region (Petals) in terms of x? Calculate the area using the dimension in 2nd figure?

1 Answer
Jul 29, 2016
Area
Explanation:
The area of half a petal is given by
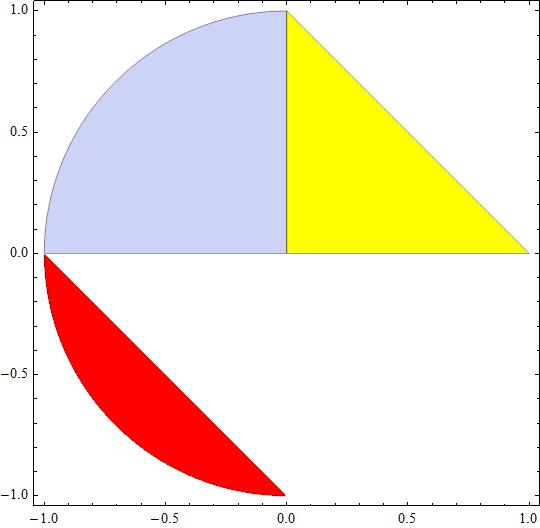
See the attached figure:
in light blue is represented the circle's quarter
in yellow is represented the triangle's area
in red is represented the difference
(Note: the halfed petal is rotated
so the four petals have an area of
Area