Please answer my question. It is optional maths?
The vertices of ▲ A(2,-3), B(5,-5) and C(3,0). ▲ ABC is translated through vector (2,-3)' to get the image ▲A'B'C' and ▲A'B'C is rotated through quarter turn in anticlockwise direction about origin to get image ▲A"B''C''. Find the coordinates of the vertices of ▲A'B'C and ▲A''B''C'' and plot it in graph?
The vertices of ▲ A(2,-3), B(5,-5) and C(3,0). ▲ ABC is translated through vector (2,-3)' to get the image ▲A'B'C' and ▲A'B'C is rotated through quarter turn in anticlockwise direction about origin to get image ▲A"B''C''. Find the coordinates of the vertices of ▲A'B'C and ▲A''B''C'' and plot it in graph?
1 Answer
The vertices of
Explanation:
Warning : Long answer
The vertices of
Translation vector
When the translation vector,
The vertices of
Under rotation about origin through quarter turn in anticlockwise direction
The vertices of
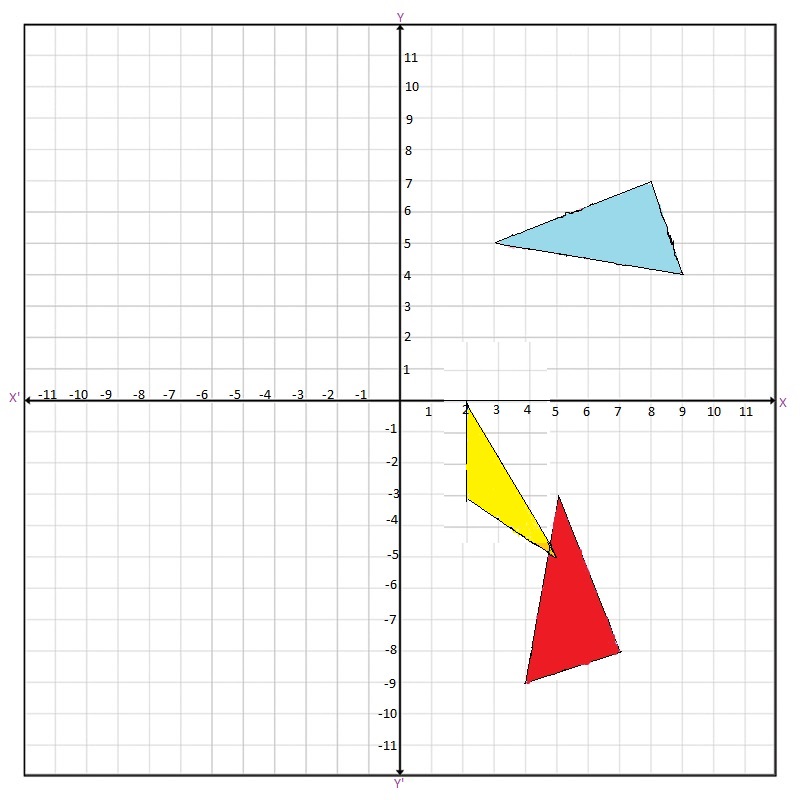
Here, yellow colored triangle represents
Red colored triangle represents
Blue colored triangle represents
Hope it helps :)

