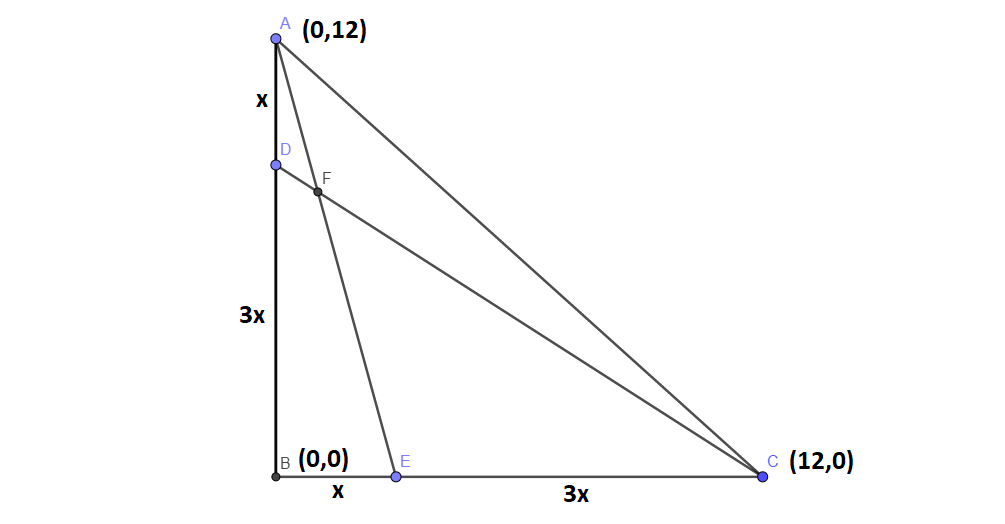
As the type of triangle is not mentioned in the question, I would take a right angled isosceles triangle right angled at B with A(0,12), B(0,0) and C(12,0) .
Now , the point D divides AB in the ratio 1:3,
So, D(x,y)=((m_1x_2+m_2x_1)/(m_1+m_2), (m_1y_2+m_2y_1)/(m_1+m_2))
=((1*0+3*0)/(1+3),(1*0+3*12)/(1+3))=(0,9)
Similarly, E(x,y)=((m_1x_2+m_2x_1)/(m_1+m_2), (m_1y_2+m_2y_1)/(m_1+m_2))
=((1*12+3*0)/(1+3),(1*0+3*0)/(1+3))=(9,0)
Equation of line passing through A(0,12) and E(3,0) is
rarry-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)
rarry-12=(0-12)/(3-0)(x-0)
rarr4x+y-12=0.....[1]
Similarly, Equation of line passing through C(12,0) and E(0,9) is
rarry-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)
rarry-0=(9-0)/(0-12)(x-12)
rarr3x+4y-36=0.....[2]
Solving [1] and [2] by the rule of cross multiplication, we get,
rarrx/(4xx(-2)-(-36)xx1)=y/(-3xx(-12)+4xx(-36)=)=1/(3-4*4)
rarrx=12/12 and y=108/13
So, the co-ordinates of F is (12/13,108/13).
Now, (CF)^2/(FD)^2=((12/13-12)^2+(108/13-0)^2)/((0-12/13)^2+(9-108/13)^2)=(144^2+108^2)/(12^2+9^2)=144=12^2
So, (CF)/(FD)=12



