Please solve q 64 ?

1 Answer
May 11, 2018
Explanation:
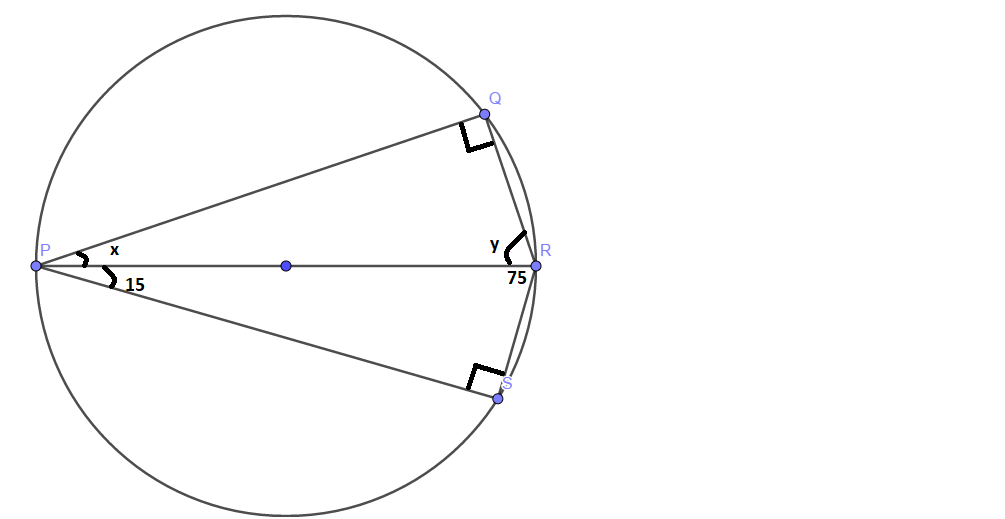
Given that,
Let
In
If three numbers
So,
and
From [1],
Putting the value of
So, the correct option is (1).


Given that,
Let
In
If three numbers
So,
and
From [1],
Putting the value of
So, the correct option is (1).