Please solve q 95 ?
![![enter image source here]](https://useruploads.socratic.org/Rsq1QOLDTOiBD6302RXh_IMG-20180511-WA0024.jpg) ![enter image source here] (
![enter image source here] ( useruploads.socratic.org)
useruploads.socratic.org)
![![enter image source here]](https://useruploads.socratic.org/Rsq1QOLDTOiBD6302RXh_IMG-20180511-WA0024.jpg) ![enter image source here] (
![enter image source here] ( useruploads.socratic.org)
useruploads.socratic.org)
1 Answer
May 12, 2018
The length of the longest side is
Explanation:
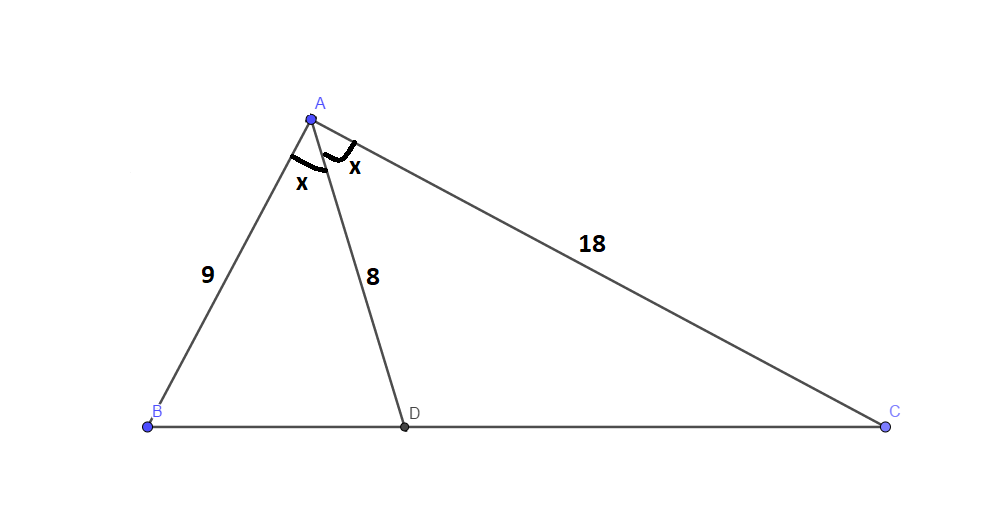
In a
Now,
Applying cosine law in
Also, note that

