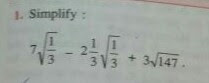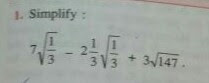We will use the fact that #sqrt(a/b)=sqrta/sqrtb#
#7*sqrt1/sqrt3-7/3*sqrt1/sqrt3+3sqrt147#
#=7/sqrt3-7/(3sqrt3)+3sqrt147#
#=(7sqrt3)/3-(7sqrt3)/9+3sqrt147#
#=(21sqrt3)/9-(7sqrt3)/9+3sqrt147#
#=(14sqrt3)/9+3sqrt147#
I've left the #3sqrt147# up till now, cos its nasty to deal with. However, seeing that we have an expression with #sqrt3#, there's a good chance that 147 will be equal to three times a square number. Some good ol' bus shelter long division (or using a calculator if you're allowed) will show you that #147=3xx49# Since 49 is a square number, we can work on simplifying this more
#=(14sqrt3)/9+3[sqrt(3xx49)]#
#=(14sqrt3)/9+3(7sqrt3)#
#=(14sqrt3)/9+21sqrt3#
#=(14sqrt3)/9+(189sqrt3)/9#
#=203/9sqrt3#