Please solve this question of mechanics?
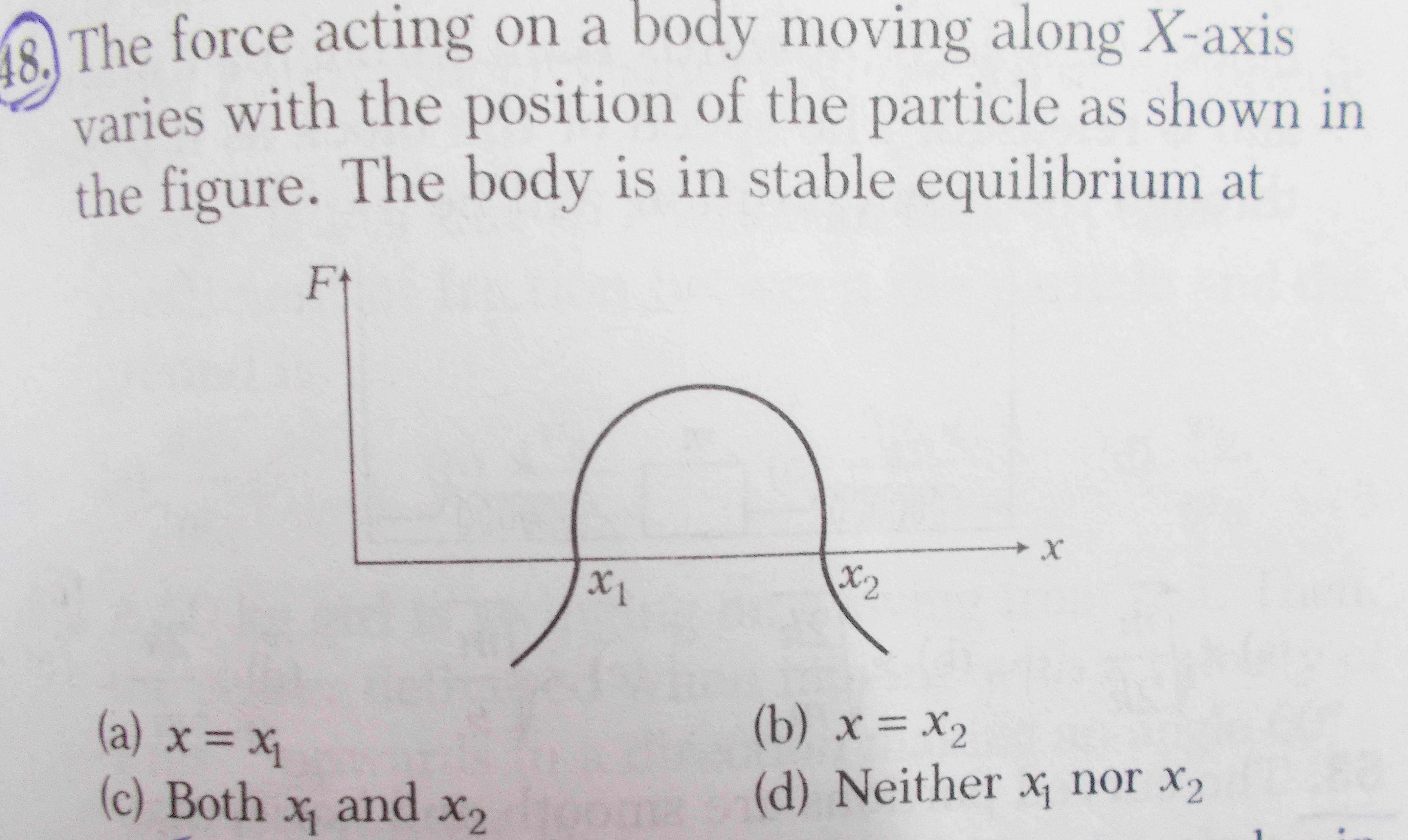 I am confused and no idea to solve this question
I am confused and no idea to solve this question
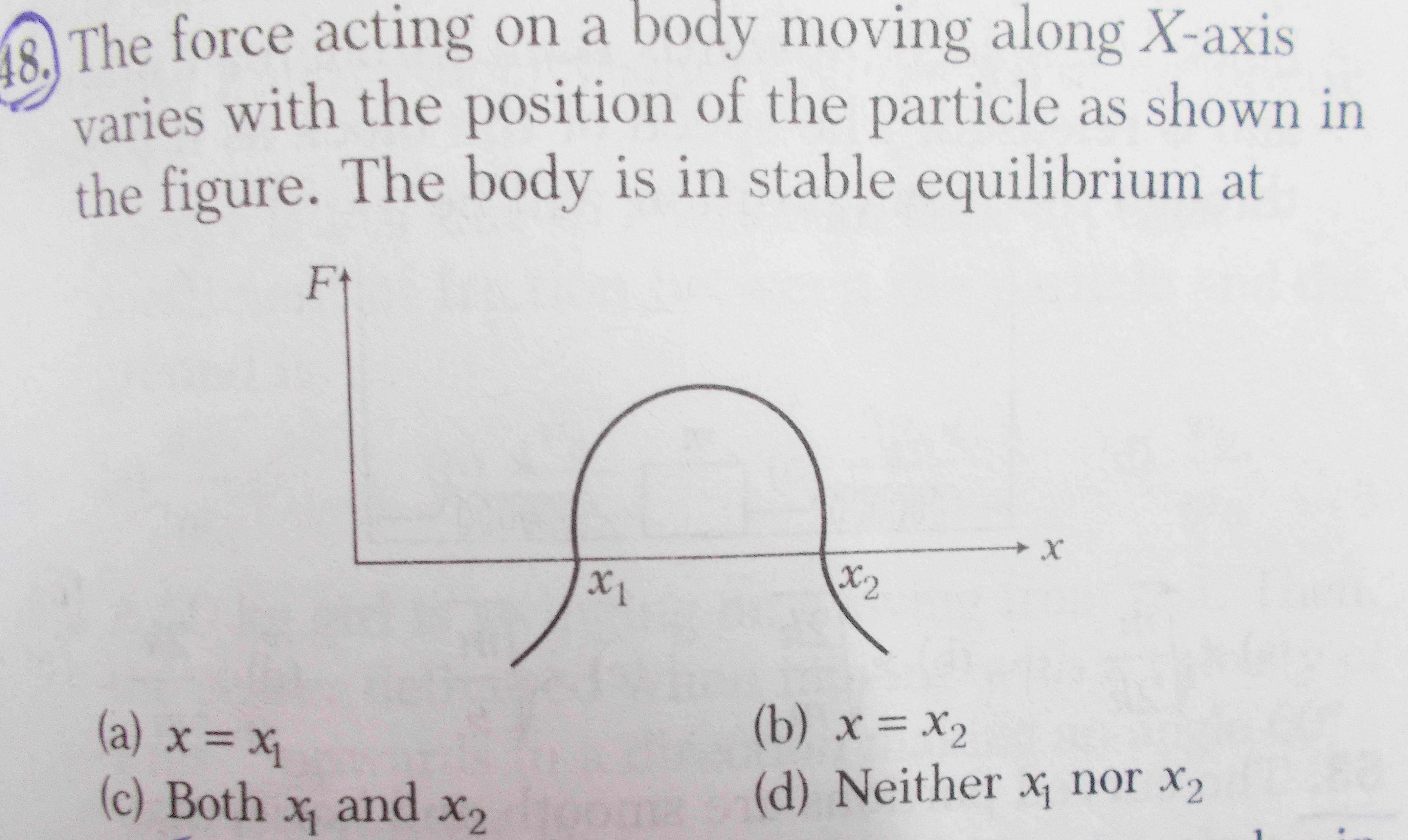 I am confused and no idea to solve this question
I am confused and no idea to solve this question
1 Answer
The stable point is
Explanation:
Considering the movement axis origin at
where
Solving for
multiplying by
then in the case of
This means also that the kinetic energy increases as the point goes away from
Analogously at point
and then
which defines a center or harmonic movement around
With dissipation the point finishes the movement at

