Point A is at #(2 ,9 )# and point B is at #(1 ,-3 )#. Point A is rotated #pi # clockwise about the origin. What are the new coordinates of point A and by how much has the distance between points A and B changed?

Question

2181 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-04T03:40:39

#color(maroon)("New coordinates of point A " (-2, -9)#

#color(purple)("Distance between A & B reduced by " color(red)(5.33 units " after point A was rotated by "pi^c#

#A (2,9), B ((1,-3)#

#bar (AB) = sqrt((x_b-x_a)^2 + (y_b - y_a)^2)#

#bar(AB) = sqrt((1-2)^2 + (-3-9)^2) = 12.04#

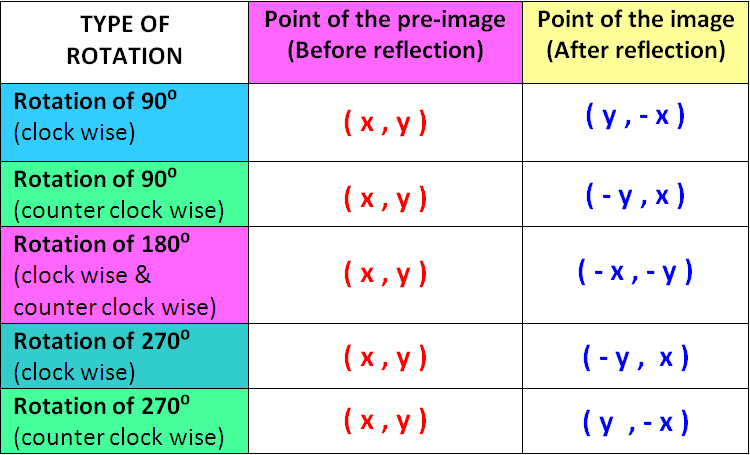
Point A rotated by #pi^c# to point A' with new coordinates,

#A' (x,y) = (-2,-9)#

#bar(A'B) = sqrt(1+2)^2 + (-3+9)^2) = 6.71#

Change in distance between #bar(AB), bar(A'B) # is

#bar(AB) - bar(A'B) = 12.04 - 6.71 = 5.33#