Point A is at #(5 ,-2 )# and point B is at #(-2 ,5 )#. Point A is rotated #pi/2 # clockwise about the origin. What are the new coordinates of point A and by how much has the distance between points A and B changed?
1 Answer
See below.
Explanation:
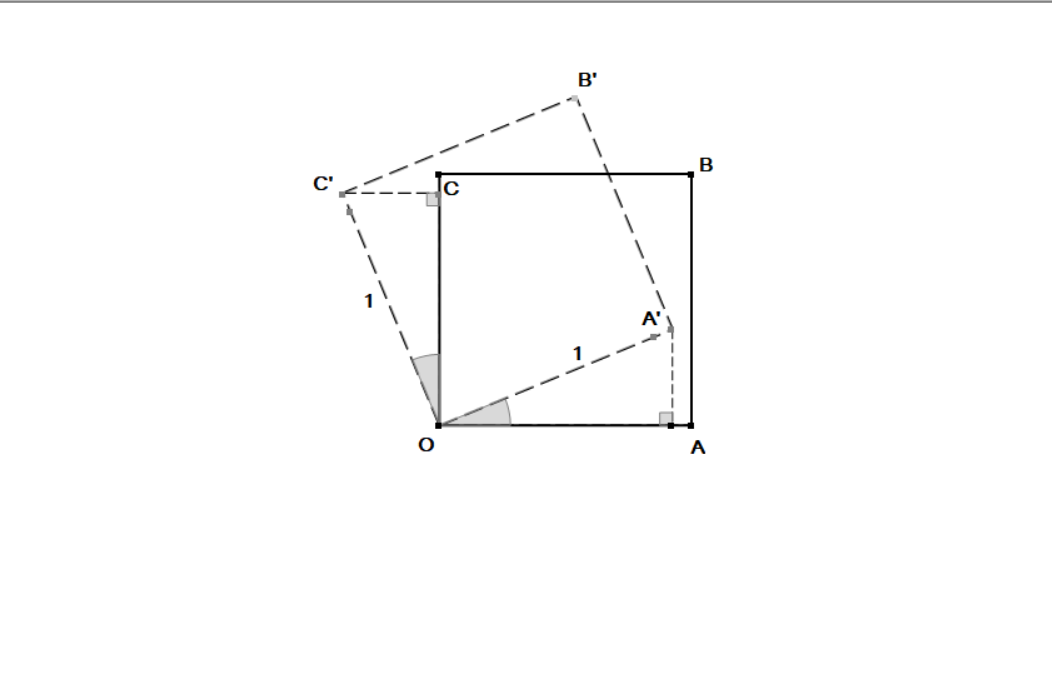
It can be seen from the diagram, that a rotation about the origin through an angle
So the transformation matrix will be:
Matrix for point A:
Transformation:- Rotation through
Distance between A and B:
Distance between A' and B:
The distance between the points has increased by a factor of

