Points A and B are at #(4 ,7 )# and #(3 ,9 )#, respectively. Point A is rotated counterclockwise about the origin by #(3pi)/2 # and dilated about point C by a factor of #4 #. If point A is now at point B, what are the coordinates of point C?
2 Answers
Explanation:
New coordinates of A after
Explanation:
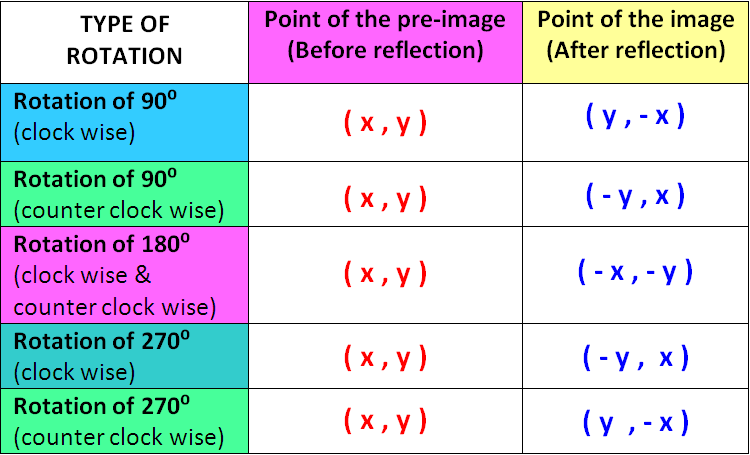
#"under a counterclockwise rotation about the origin of "(3pi)/2#
#• " a point "(x,y)to(y,-x)#
#A(4,7)toA'(7,-4)" where A' is the image of A"#
#vec(CB)=color(red)(4)vec(CA')#
#ulb-ulc=4(ula'-ulc)#
#ulb-ulc=4ula'-4ulc#
#3ulc=4ula'-ulb#
#color(white)(3ulc)=4((7),(-4))-((3),(9))#
#color(white)(3ulc)=((28),(-16))-((3),(9))=((25),(-25))#
#ulc=1/3((25),(-25))=((25/3),(-25/3))#
#rArrC=(25/3,-25/3)#
