Projectile launcher problem?
A projectile launcher is set on a table so that the ball becomes a projectile at a height of 1.2 meters above the floor. The mass of the ball is 10 grams (0.01kg). A plunger is used to push the ball into the barrel of the launcher, compressing the spring a distance of 10 cm (.10m) before it is ready to launch. It is launched at an angle of 30 degrees above the horizontal. The ball travels a horizontal distance of 4 meters before striking the floor below. Determine the force constant of the spring that shot the ball in this fashion.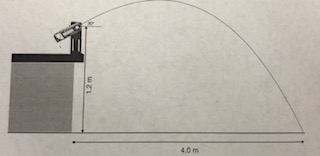
A projectile launcher is set on a table so that the ball becomes a projectile at a height of 1.2 meters above the floor. The mass of the ball is 10 grams (0.01kg). A plunger is used to push the ball into the barrel of the launcher, compressing the spring a distance of 10 cm (.10m) before it is ready to launch. It is launched at an angle of 30 degrees above the horizontal. The ball travels a horizontal distance of 4 meters before striking the floor below. Determine the force constant of the spring that shot the ball in this fashion.
1 Answer
Explanation:
Let
where
Follows the
so the non-parametric orbit equation is
now
but
with
Now solving for
with
giving
and finally

