Show that the roots of the equation #16x^4 - 20x^2 + 5= 0# are #cos((kx)/10) #for #k = 1,3,7 # and # 9# And Deduce that #cos^2(pi/10)cos^2((3pi)/10) = 5/16#?
2 Answers
Antoine, I think that your roots are without
To solve your equation substitute
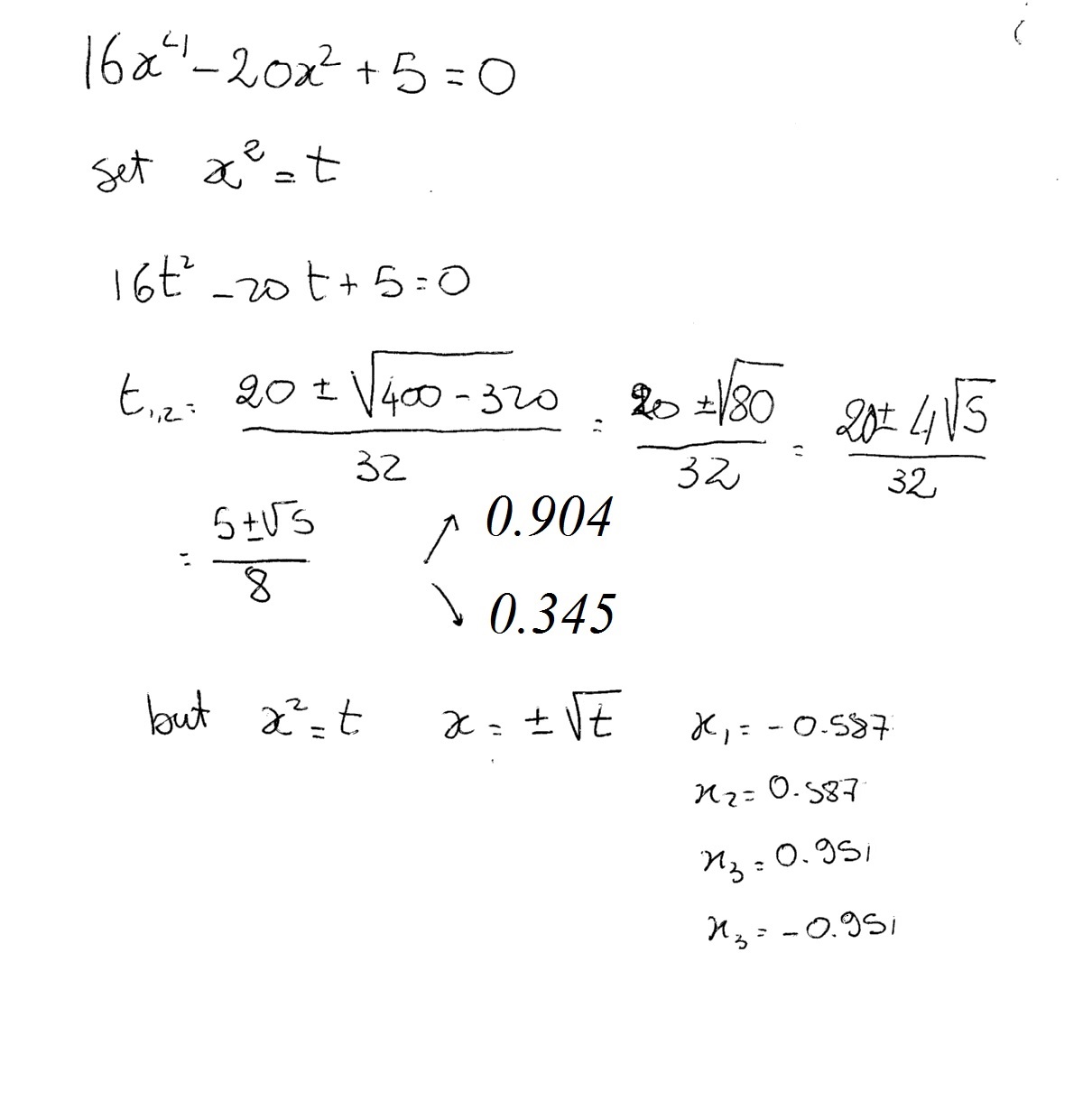
Your roots corresponds to
and if you have:

Has real zeroes, because
For the full solution, see Gio's answer.)
The factor theorem gives us:
The constant for this product is clearly
Therefore,
For the first part
Expand
Then with
In fact, with


