Solve for the variables in each of the diagrams?

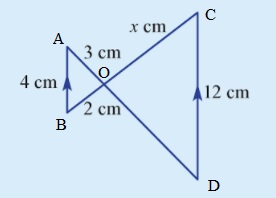
enter image source here

enter image source here

1 Answer
Shwetank Mauria
Aug 2, 2017
  1. #x=6# #cm.#
  2. #a=70#, #b=c=55#

Explanation:

Ques.No.1
enter image source here
In #DeltasABO# and #COD#

#/_AOB=/_COD# - vertically opposite angles
#/_ABO=/_DCO# - alternate opposite angles as #AB#||#CD#
#/_BAO=/_ODC# - alternate opposite angles as #AB#||#CD#

As such #DeltasABO# and #COD# are similar and hence

#(CO)/(OB)=(CD)/(AB)# i.e. #x/2=12/4#

and #x=12/4xx2=6# #cm.#

Ques.No.2
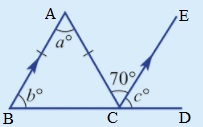
enter image source here
As #AB#||#CE# and #AC# is transverse #/_a=70^@# as they are alternate interior angles.

Further as #AB#||#CE# and #BC# is transverse #/_b=/_c# as they are corresponding angles.

Now in #DeltaABC#, we have #AB=AC#, hence #/_ACB=/_ABC=b^@#

Hence #2b^@+a^@=2b^@+70^@=180^@#

or #2b^@=180^@-70^@=110^@# i.e. #b=55#

and as #/_c=/_b=55^@#, #c=55#

Related questions
Impact of this question
834 views around the world
You can reuse this answer
Creative Commons License