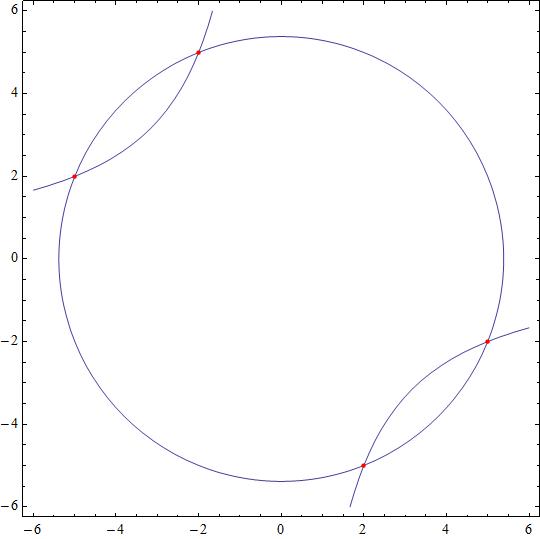
Solve the following system of equations: (x^2+y^2=29),(xy=-10)(x2+y2=29),(xy=−10) ?
Solve the following system of equations:
[(1 " ", x^2+y^2=29),(2 " ", xy=-10)] ?
Solve the following system of equations:
1 Answer
Jun 10, 2016
The solutions are
Explanation:
Substituting for
Making
With the final solutions
The attached figure shows the intersection points of