Cardioid Curves
Key Questions
-
Answer:
A cardioid
Explanation:
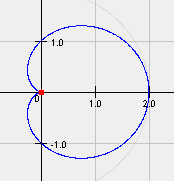
This is a cardioid.
We can observe that the positive/negative just flip the orientation of the figure since cosine goes from -1 to 1 either way. Let's just discuss the negative case for now, but remember that it doesn't really matter (it just rotates it by an angle of 180 degrees)
We observe that there is an angle where the value goes all the way to 0 (
#theta = 0# ). This is a cusp at the same angle every time. For every other value, the angle is positive, all the way up to the opposite side (#theta = pi# ) where it is#2a# away from the center. This means that the function kinda looks like a heart (hence the name cardioid). Here's a plot of one:graph{ sqrt(x^2+y^2) = x^2 + y^2 + x [-4, 1, -1.5, 1.5]}
Jake M. · 1 · Aug 14 2018
-
Answer:
Please see below
Explanation:
Cardioid curve is some thing like a heart shaped figure (that is how the word 'cardio' has come). It is the locus of a point on the circumference of a circle that moves on another circle without slipping.
Mathematically it is given by the polar equation
#r=a(1-costheta)# , at times also written as#r=2a(1-costheta)# ,It appears as shown below.
Shwetank Mauria · 1 · Mar 23 2016