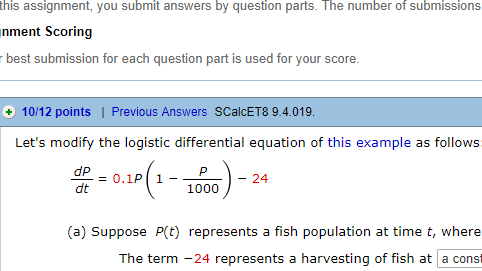
Solve this differential equation explicitly, either by using partial fractions, or with a computer algebra system. Use the initial populations 350 and 450. Can anyone please help me with this problem and explain how you got the answers?
1 Answer
For the IV:
# P= 100 ((e^( t/50) + 5)/(e^( t/50) - 5) + 5 )#
For the IV:
# P= 100 (( e^( t/50) - 3)/( e^( t/50) + 3 ) + 5 )#
Explanation:
Complete square:
Let
So the DE is:
Let
This separates:
Factor and use partial fractions:
Reverse the subs:
For the IV:
For the IV:

