Question

When considering a competitive market for apartments in a city. What would be the effect on the equilibrium price and output after the following changes (other things being held constant):?

a) A rise in the income of consumers.
b) A new construction technique allowing apartments to be built at half the cost.

Answer 1

Refer Explanation Section

Explanation:

The market is competitive.
Other things remain unchanged.

a) A rise in the income of consumers.

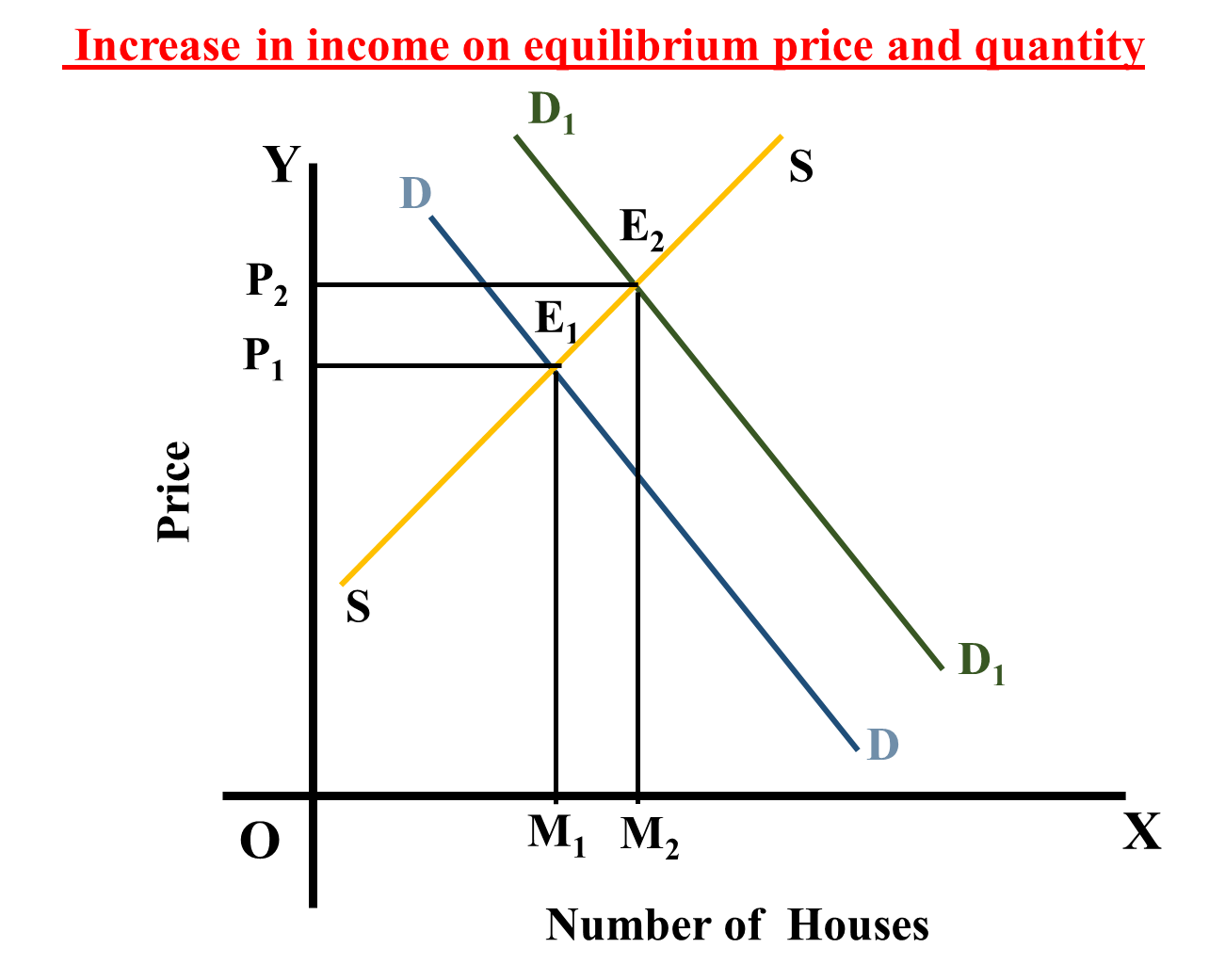
To begin with the demand for and supply of houses determine the equilibrium price and number of houses.`DD` is the demand curve. `SS` is the supply curve. They become equal at point `E_1`. `E_1` is the equilibrium point. `M_1` number of houses are supplied and demanded at `P_1` Price.

After an increase in the income of the consumers, The demand curve is shifted to right. The new demand curve is `D_1 D_1`. It cuts the supply curve `SS` at point `E_2`

The new equilibrium Price is `P_2`. This is higher than the original price.

The new equilibrium number of houses is `M_2`. This is greater than the original number of houses.

The Net result is a rise in price and number of houses.

b) A new construction technique allowing apartments to be built at half the cost.

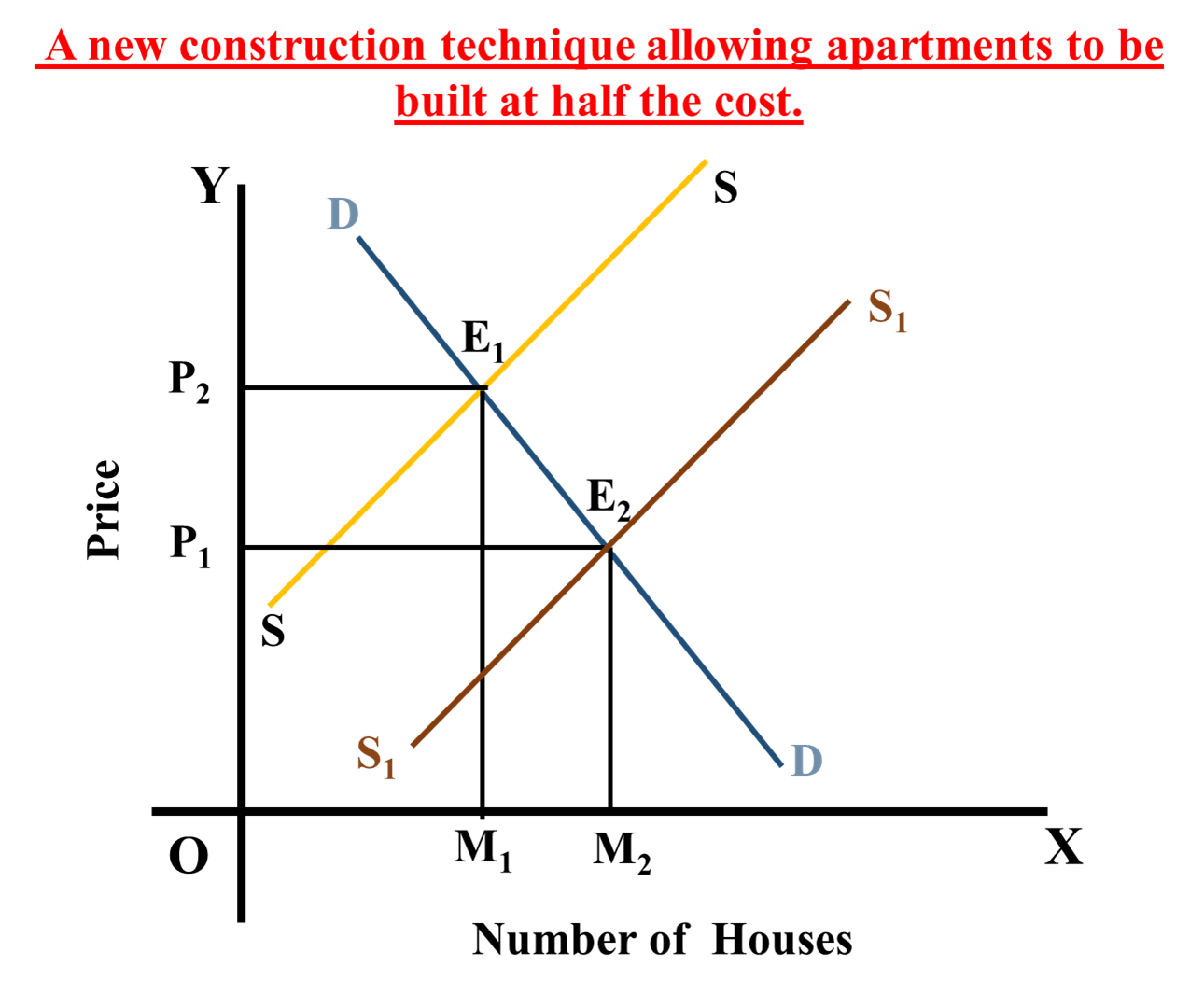
The initial equilibrium is at point `E_1`. Equilibrium price is `P_2`. Equilibrium number of houses is `M_1`

With an improvement in technology, the supply curve will be shifted to right. The New supply curve is `S_1S_1`.

The new equilibrium point is `E_2`

The new equilibrium price is `P_1`. This is less than the original price.

The new equilibrium number of houses is `M_2`. This is greater than `M_1`.

The net result is a decrease in price and an increase in number of houses.