Strong base weak acid titration?
A 35.0 mL sample of 0.150 M acetic acid (CH3COOH) is titrated with 0.150 M NaOH solution.
Calculate the pH after the following volumes of base have been added:
a) 34.5mL
b) 35.0mL
A 35.0 mL sample of 0.150 M acetic acid (CH3COOH) is titrated with 0.150 M NaOH solution.
Calculate the pH after the following volumes of base have been added:
a) 34.5mL
b) 35.0mL
1 Answer
Explanation:
The ethanoic acid is neutralised by the sodium hydroxide:
We find the initial moles of ethanoic acid:
Then we find the no. moles NaOH added:
From the equation we can see that for every mole of
We are in the buffering region of the titration. Ethanoic acid is a weak acid and dissociates:
For which:
(I had to look this up - you would be given it in a question)
These are equilibrium concentrations.
Rearranging:
Because the dissociation is so small we can make the assumption that the moles we have calculated approximate to the equilibrium moles.
Since the total volume is common to acid and co - base we can put moles straight into the equation:
Now we are at the equivalence point. This is where the reactants are in the molar ratio as specified by the equation.
We know that the initial moles of
So the number of moles of
We need to find the concentration using
Note that the total volume is 35.0 + 35.0 = 70.0 ml which I have converted to litres.
So now we have a 0.075 M solution of sodium ethanoate for which we need the pH.
You might think that, because the acid has been neutralised, the pH should be 7. However, this is not the case for the titration of a weak acid and a strong base.
The ethanoate ions undergo hydrolysis:
This means we would expect the resulting solution to be alkaline.
If you rearrange the expression for
Again, we assume that, because the dissociation is small, the equilibrium concentration of
We can get
We know that:
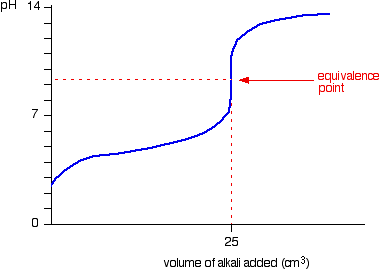
As you can see this is alkaline. The pH curves illustrates this:
 chemguide.co.uk
chemguide.co.uk

