Question

Test the series for convergence or divergence. In each case give reasons for your decision?

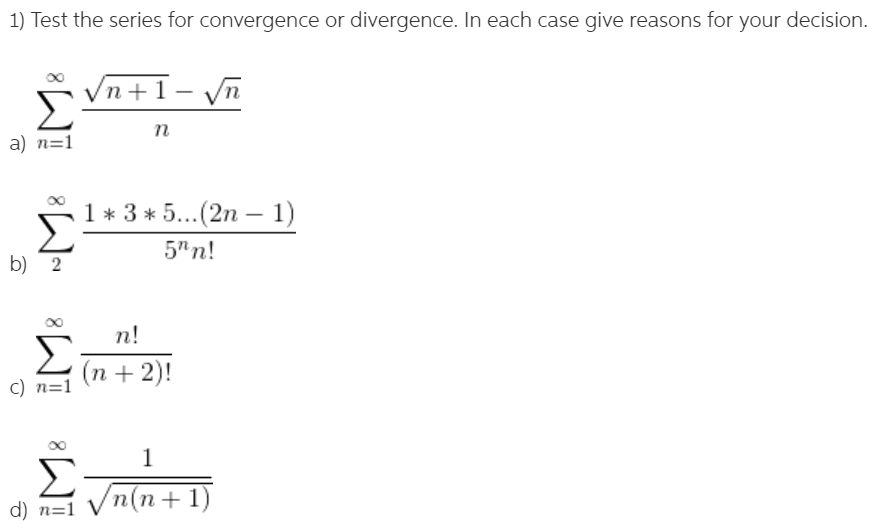
For part a), the ratio test and root test both come back inconclusive. The only option is to use the comparison test, which wolfram alpha says will give a convergence.

Please show work and explain! I'm so lost

Answer 1

a) Consider

`lim_(n ->oo) sqrt(n + 1)/n`

This converges to `0`. Thus, `sum_(n = 1)^oo sqrt(n + 1)/n` converges.

`lim_(n-> oo) (sqrt(n + 1) - sqrt(n))/n` must converge to `0` even quicker. Thus `sum_(n = 1)^oo (sqrt(n + 1) - sqrt(n))/n` must converge.

I'll leave the other ones up to other contributors.

Hopefully this helps!