The area of the parallelogram is 150 sq. in. What is the perimeter given the height is 6 and the base is 4x-3?
1 Answer
Oct 26, 2016
The formula for area of a parallelogram is
So, the base measures
Let's draw a diagram.
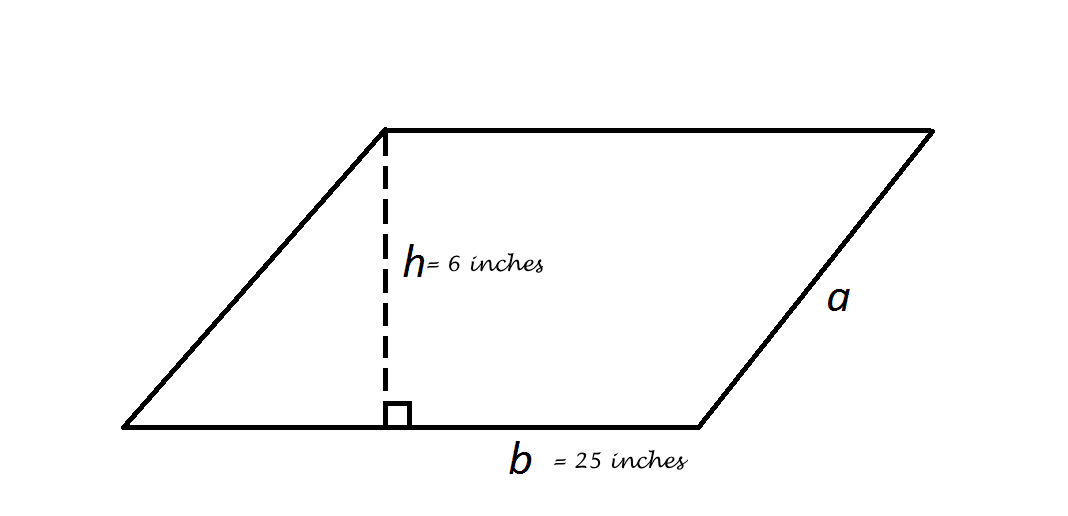
So, we need to find
By pythagorean theorem:
The perimeter is simple to find now:
Hopefully this helps!

