The astrological configuration of a party with n guests is a list of twelve numbers that records the number of guests with each zodiac sign. How many different astrological configurations are possible for n = 100?
How many astrological configurations are possible for n = 100, if each component is at least 5?
How many astrological configurations are possible for n = 100, if each component is at least 5?
3 Answers
I got
Explanation:
I think I'm reading the question correctly by saying that having 45 numbers associated with one astrological sign, say Leo, and 5 in all the others is the same as having 45 numbers associated with say Taurus and all the others have 5 (and so I'm assuming that it's the list of numbers that we're interested in and not the numbers of people associated with each sign).
If that is true, what we're dealing with are identical items (numbers or people) going into identical groupings (the list of numbers). This type of question can be solved by using Partitions, or in other words looking at the number of ways we can add numbers up to to larger numbers.
For instance, the partition of the number 5 is 7:
For our question, we can take the
There are no easy ways at this time to work with partitions - most of the time computers are used to do the calculations once they reach what might seem to be a small number. For our calculation, I used a partition widget at Wolfram Alpha:
http://www.wolframalpha.com/widgets/view.jsp?id=ca10ab4a89d9f0f6f378b89881f63ba3
If we were to do a full partition of the number 40, we'd have 37,338 ways to arrange the list. However, we're only interested in partitions that have, at most, 12 buckets. Luckily, the widget has the ability to look at that:
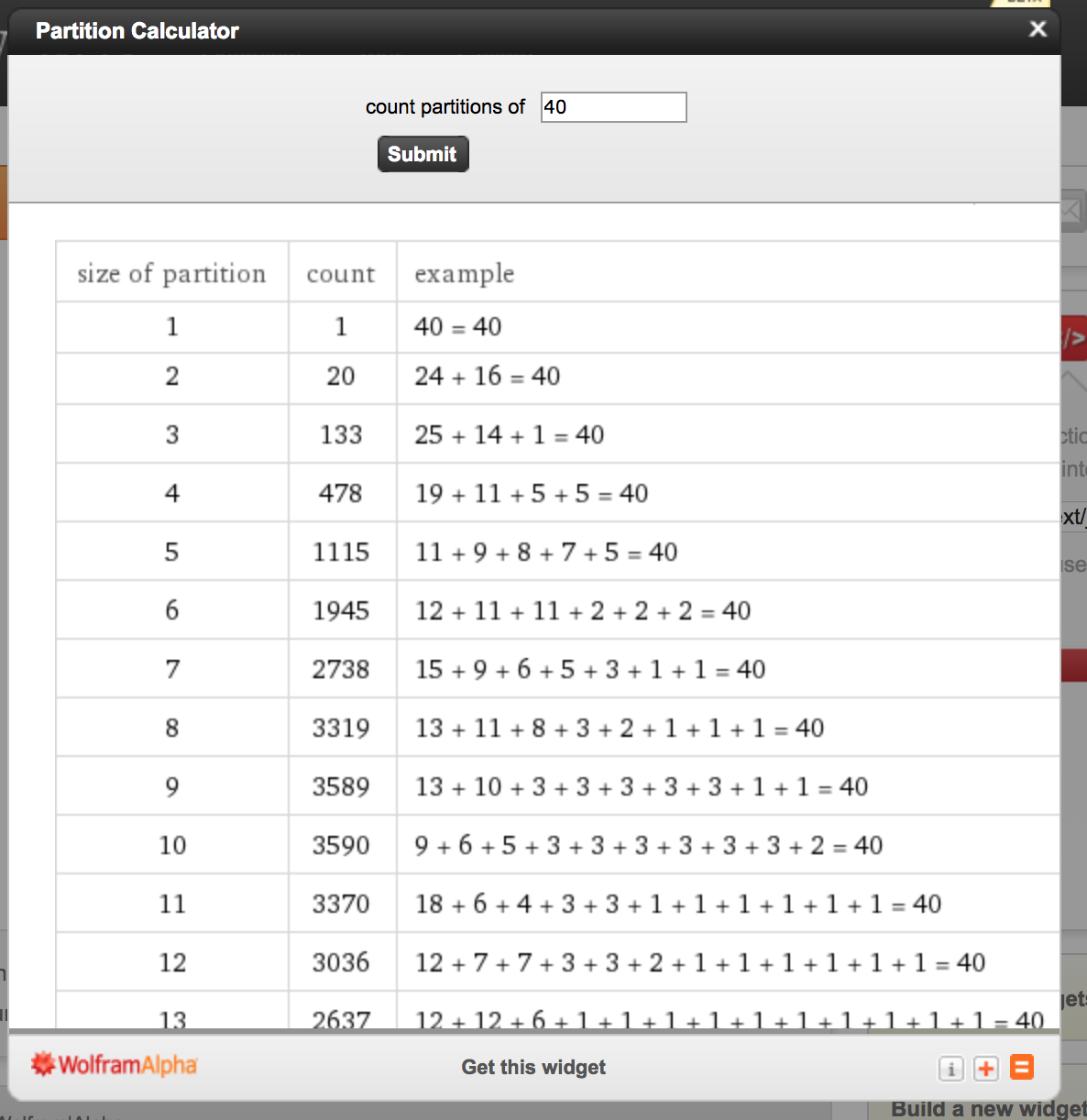
We can add up the counts of the partitions up to and including 12 and end up with
If the items (numbers of people) are identical but the categories are distinct, we have
Explanation:
I'm writing this answer to cover the possibility that we're dealing with putting identical items (the numbers of people) into distinct/unique categories (and so having 45 people in Leo and 5 in all other astrological signs) is different that having 45 people in Taurus and 5 in all the other signs.
If that is true, what we're dealing with are identical items (numbers or people) going into identical groupings (the list of numbers). This type of question can be solved by using "stars and bars", or in other words lining up the items to be categorized (the numbers of people) and grouping them using moving walls.
For instance, let's take four things (which we can denote using a symbol - I'll use capital P):
PPPP
and find the number of ways we can arrange them across 3 categories. To define the categories, we use "bars" - or essentially walls to separate the stars into groups. Here's one arrangement:
P | PP | P (which has one group of two Ps and two groups of one P each)
and here's another:
|||PPPP (which has a single group of four Ps and two empty baskets).
What we then end up with is the combination general formula of:
where
For our question, we'll use the same analysis of having 60 people already placed and so we're looking for the number of ways to arrange the other 40 people across 12 categories. That gives:
A supplementary answer, assuming individuals are distinct.
Explanation:
This last answer will cover the two cases where the individuals we're grouping are distinct (and so we're not working with numbers of people here but with actual names of people being grouped. It'd be quite a stretch for this answer to directly answer the question as it seems to read for identical items being grouped but I thought I'd include it here, if only for the curious.
Distinct items into identical groupings
Let's say at the party the 100 people group themselves together. At this point all we care about is that the people are grouped, not the signs around which they are grouped.
To find the number of ways to create this configuration, we first look at the 60 people that are forced to be in 12 groups of 5.
I'm going to look at this in the following way - we can take the permutation of 100 select 60, which will in essence "line up" 60 people in a line with someone being first, someone being second, etc. We can take the first 5 people as the first grouping of a sign, the next 5 the next grouping of a sign, etc. So that's:
Keep in mind that we're going to have duplicates - these groupings are combinations (we don't care in what order they are picked) and so to eliminate them we divide through by the number of ways we can have duplicates. That's
Now we work with the 40 people left to group. We found in the answer dealing with identical items going into identical groups that we needed to use partitions and that the partition of 40 into 12 terms or less is 23,334. This is the number of ways we can arrange the 40 people across the different groups.
To find the number of ways we can put the individuals across these places, we multiply by the number of ways we can arrange them, which is
All together then, we have:
~~~~~~~~~~
Distinct items into identical groupings
If we include the names of the astrological houses to which everyone is grouped, we now have the same basic logic as above but instead of multiplying
This gives:

