The base of a certain solid is the triangle with vertices at (-8,4), (4,4), and the origin. Cross-sections perpendicular to the y-axis are squares. How do you find the volume of the solid?

Question

18477 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-15T21:47:29

Please see below.

Here is a picture (graph) of the base (in blue) with a thin slice taken perpendicular to the #y#-axis (in black).

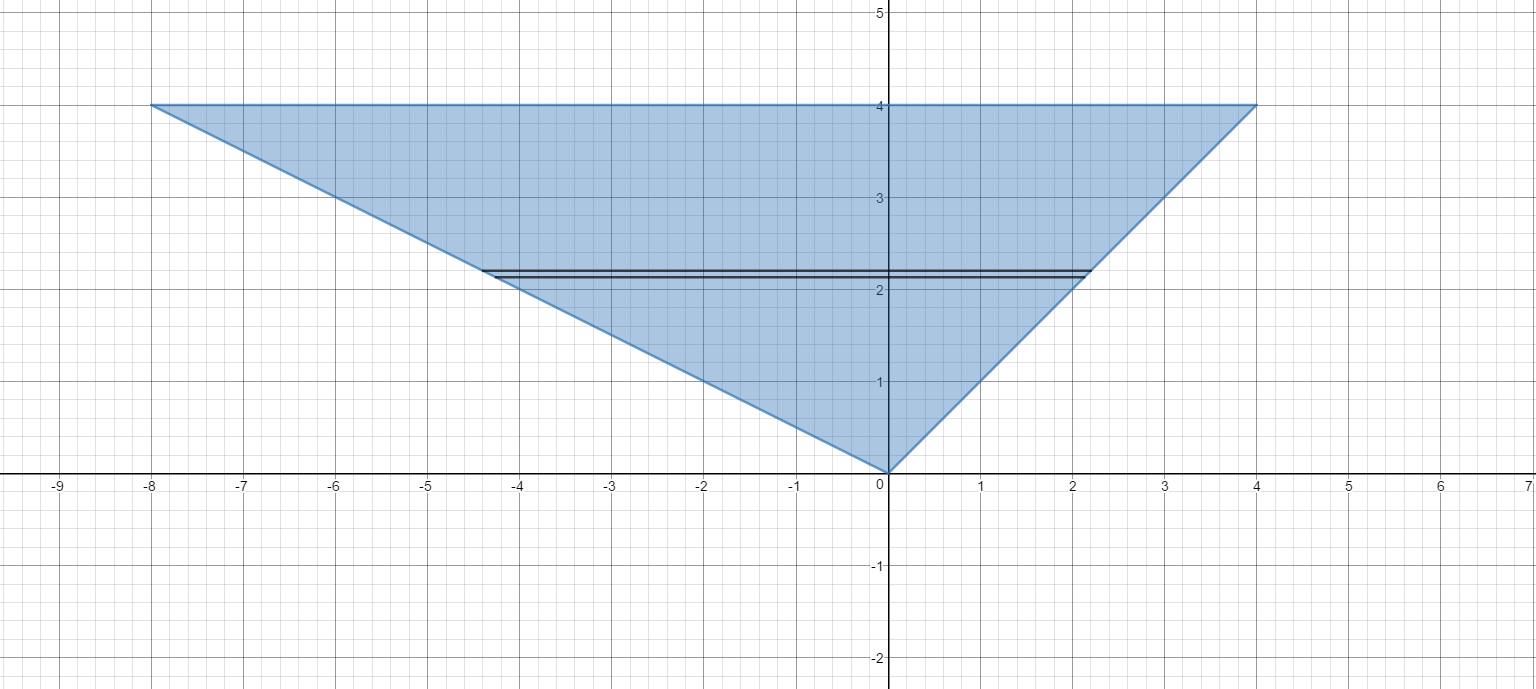
enter image source here

The thinkness of this representative slice is #dy# so we need the sides of the square to be expressed in terms of #y# (not #x#).

The line on the right contains #(0,0)# and #(4,4)#. Its equation is #y = x# or #x = y#

The line on the left contains #(0,0)# and #(-8,4)#. Its equation is #y = -1/2x# or #x = -2y#

The side of the square built on the representative slice is #s = x_"greater"-x_"lesser" = x_"on the right"-x_"on the left"#.

So, #s = y - (-2y) = 3y#.

The volume of the representative slice is

#s^2 * "thickness" = (3y)^2 dy#.

The values of #y# vary from #0# to #4#, so the volume of the solid is

#V = int_0^4 (3y)^2 dy = {:3y^3]_0^4 = 192# (cubic units)