The bolts on a car wheel require tightening to a torque of 90 N-m. If a 30 cm long wrench is used, what is the magnitude of the force required when the force applied at 53° to the wrench?
1 Answer
The force required is 376 N
Explanation:
We will use the principle of moments to solve the problem. The question tells us that the force on the wrench needs to supply 90 Nm of torque to the bolt. It supplies the lever arm length (30 cm) and the angle at which the force acts (53º to the wrench).
Here is a diagram of the situation (please note how I have interpreted the angle):
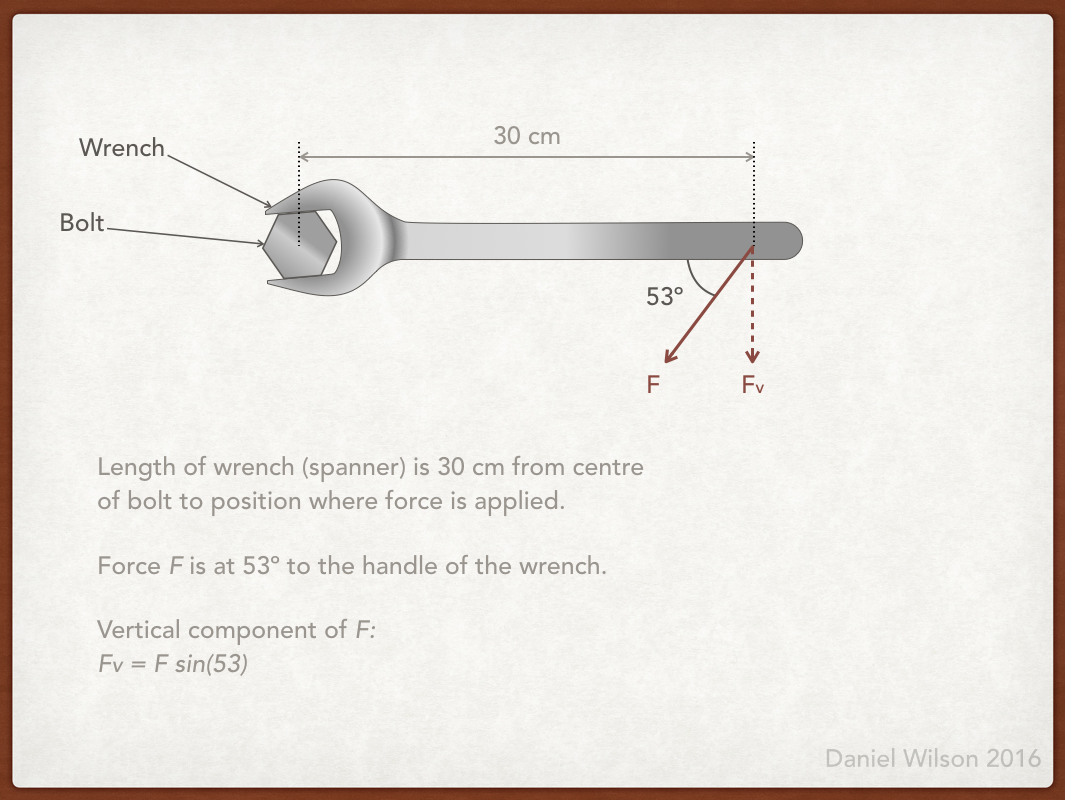
Before we get into the main part of the calculations a conversion. The length of the wrench is given in centimetres, that needs converting to metres:
Now use trigonometry to get an expression for the vertical component of the force. The vertical component is opposite to the 53º angle so the equation is:
Lastly write the equation for the moments about the bolt. The moment of the force is the vertical component of the force multiplied by the lever arm (0.30 m). Remember that the force needs to provide a torque of 90 Nm, so that torque I will put in the left hand side of the equation.
Rearrange for F and solve:

