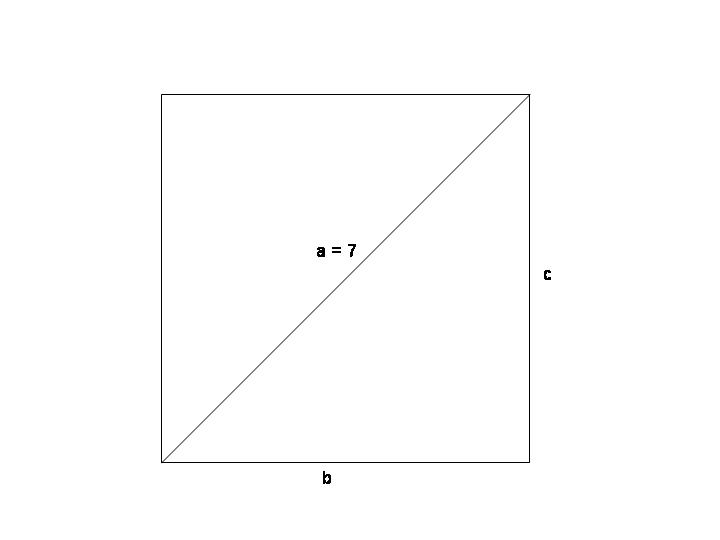
The diagonals of a square each measure 7 feet. How do you find the area of the square?
2 Answers
4.95 feet
Explanation:
You must use trigonometry.
Since it is a square, and each angle in a square is 90 degrees, the two angles of the triangle the diagonal makes is half of that, 45.
You can use the Pythagorean Theorem
Explanation:
The Pythagorean Theorem says that in a square triangle the square of the hypotenuse (a) is equal to the square of one leg (b) plus the square of the other lag (c):
The diagonal of a square form a square triangle with two of the sides (see figure below) and (b) is equal to (c). Therefore, the equation can be written as below:
The area is the product of two sides