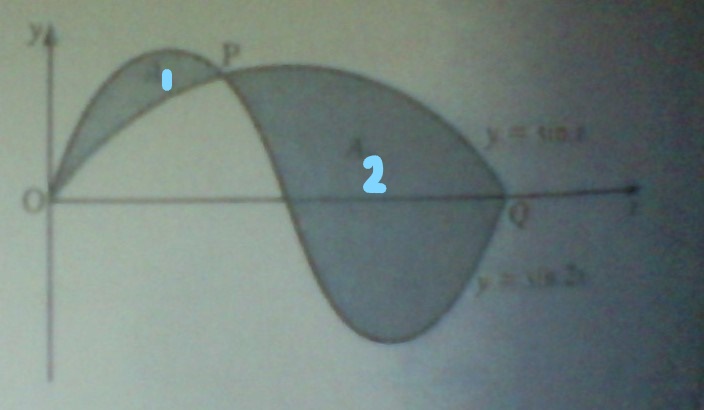
The diagram shows two curves with equations y=sin x and y=sin2x for x values between 0 and pi. the curves meet at the origin and at the points P and Q. a) find P and Q? b)find the areas of the shaded regions A1 and A2?
1 Answer
Jun 11, 2018
We need to set the two curves equal.
#sinx = sin(2x)#
#0 = sin(2x) - sinx#
#0 = 2sinxcosx- sinx#
#0 = sinx(2cosx- 1)#
#sinx= 0 or cosx = 1/2#
#x = 0, pi, pi/3#
Now we set up our integral expressions for area.
#A_1 = int_0^(pi/3) sin(2x) - sinx dx#
#A_1 = [-1/2cos(2x) + cosx]_0^(pi/3)#
#A_1 = -1/2cos((2pi)/3) + cos(pi/3) + 1/2cos(0) - cos(0)#
#A_1 = 1/4 + 1/2 + 1/2 - 1#
#A_1 = 1/4# square units.
Now onto
#A_2 = int_(pi/3)^pi sinx - sin(2x)dx#
#A_2 = [ -cosx + 1/2cos(2x)]_(pi/3)^pi#
#A_2 = -cos(pi) + 1/2cos(2pi) - (-cos(pi/3) + 1/2cos(2(pi/3))#
#A_2 = 1 + 1/2 + 1/2 + 1/4#
#A_2 = 9/4#
The total area is
Hopefully this helps!

