Question

The electron affinity of bromine is a negative quantity while it is a positive quantity for krypton, using the electron configurations of the two elements, how would you explain the difference?

Answer 1

Here's what's going on here.

Explanation:

First of all, make sure that you have clear understanding of what negative electron affinity means.

As you know, electron affinity is defined as the energy released when one mole of electrons in add to one mole of atoms in the gaseous state.

`color(blue)("X " + " e"^(-) -> " X"^(-) + "energy")`

Now, by convention, energy released is considered to be negative. This means that when adding an electron to an atom releases energy, electron affinity will actually be listed as a positive value.

`E_"a" = -DeltaE`

When electron affinity is negative, it implies that adding an electron to an atom actually requires energy.

So if you go by the sign convention, the electron affinity of bromine is actually positive because energy is being released when you add an electron to bromine.

On the other hand, krypton's electron affinity is actually negative beause you need to provide energy to add an electron to akrypton atom.

So why is that the case?

The key lies indeed with the electron configurations of the two atoms, which looks like this - I'll use the noble gas shorthand notation

`"Br: " ["Ar"] 3d^10 color(red)(4)s^2 color(red)(4)p^5`

and

`"Kr: " ["Ar"] 3d^10 color(red)(4)s^2 color(red)(4)p^6`

Notice that the outermost energy shell, which for both atoms lies on the fourth energy level, `n=color(red)(4)`, is completely occupied in krypton's case.

In other words, krypton has a complete octet - `8` electrons on its outermost shell.

On the other hand, bromine only has `7` electrons on its outermost shell, `2` in the 4s-orbital and `5` in the 4p-orbital.

Since atoms are expecially stable when they have complete octet, a significant amount of energy will be released when the incoming electron is added to bromine's outermost shell, thus giving it the aforementioned complete octet.

On the other hand, in krypton's case, the incoming electron must be added to the next energy level, `n=5`, which is so energetically unstable that energy must be provided in order to make this happen.

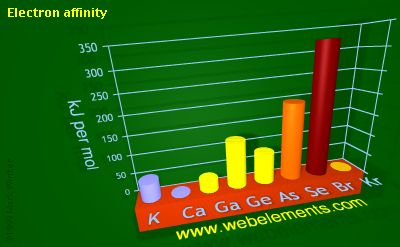
This is why krypton's electron affinity is negative `->` you'll sometimes see it listed as `0`, like you can see in the above graph.