The hypotenuse of a right triangle is 15 centimeters long. One leg is 9 cm long. How do you find the length of the other leg?
2 Answers
The other leg is
Explanation:
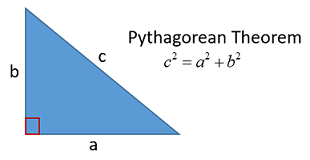
Use the Pythagorean theorem:
where:
Let
Rearrange the equation to isolate
Simplify.
Take the square root of both sides.
Simplify.
Explanation:
Since this is a right triangle, we can use the Pythagorean Theorem.
We can substitute in
So the other leg is


