Question

The locus of the centre of a circle which touches the circle `|z-z_1|=a` and `|z-z_2|=b` externally will be ?

Answer 1

The locus of the center of tangent circle is a hyperbola with `z_1` and `z_2` as focii and difference between the distances from focii is `a-b`.

Explanation:

Equations of the circles `|z-z_1|=a` and `|z-z_2|=b`

represent circle with center at `z_1` and `z_2` and radii `a` and `b`. Note that coordinates are mentioned in terms of complex number. Here geometrical representation of `z_1` is `(x_1,y_1)` and that of `z_2` is `(x_2,y_2)`.

As it is not given, we assume that these circles do not touch each other. Let the circles be - one (the bigger one i.e. `a>b`) with center `A` and passing through `B` and other with center `C` and passing through `D`.

Let the desired circle, which we may call as tangent circle (the one touching both the given circles) externally touch circle `A` at `E`. It is obvious that center of tangent circle, as it touches circle `A` at `E`, would lie on `AE` extended.

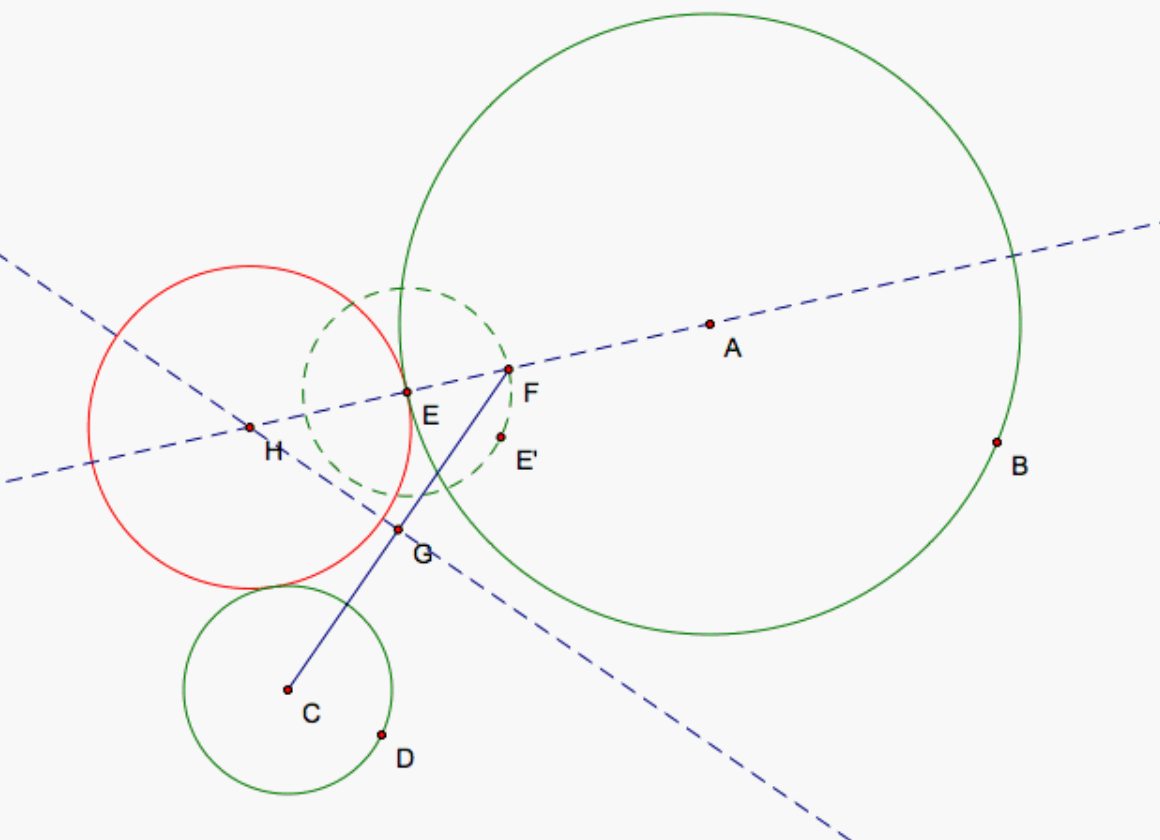
Let us draw a circle with center at `E` and having same radius as that of smaller circle, which cuts `AE` at `F`. Join `FC` and draw a perpendicular bisector of `FC`. If we draw a circle center at a point on this perpendicular bisector `OH`, it will touch smaller circle `C` and also pass through `E`.

Hence a tangent circle to circle `A` (touching it at `E`) and `C` will lie on point of intersection of `OH` and `AE` extended. Observe that

1. the distance of tangent circle `H` from circle `A` and `C` is `HC` and `HA` and difference between these distances is `a-b`,
2. If we change the point `E` to some other point on circle `A`, we will have a new circle, with different center and different radius, but difference between distances with the two circles will always be `a-b`.

Therefore, the difference of the distances of tangent circle from the centers of two given circles will always be constant and equal to `a-b`.

Hence, from the definition of hyperbola, the locus of the center of tangent circle is a hyperbola with `z_1` and `z_2` as focii and difference between the distances from focii is `a-b`.