The osmotic pressure of blood is 7.7 atm at 25°C. What concentration of glucose, #C_6H_12O_6#, is isotonic (same osmotic pressure) with blood?
1 Answer
Explanation:
The problem wants you to determine what concentration of glucose would produce a solution that has the same osmotic pressure as blood at
As you know, osmotic pressure is defined as the pressure required to prevent the flow of water across a semi-permeable membrane from a region of lower solute concentration into a region of higher solute concentration
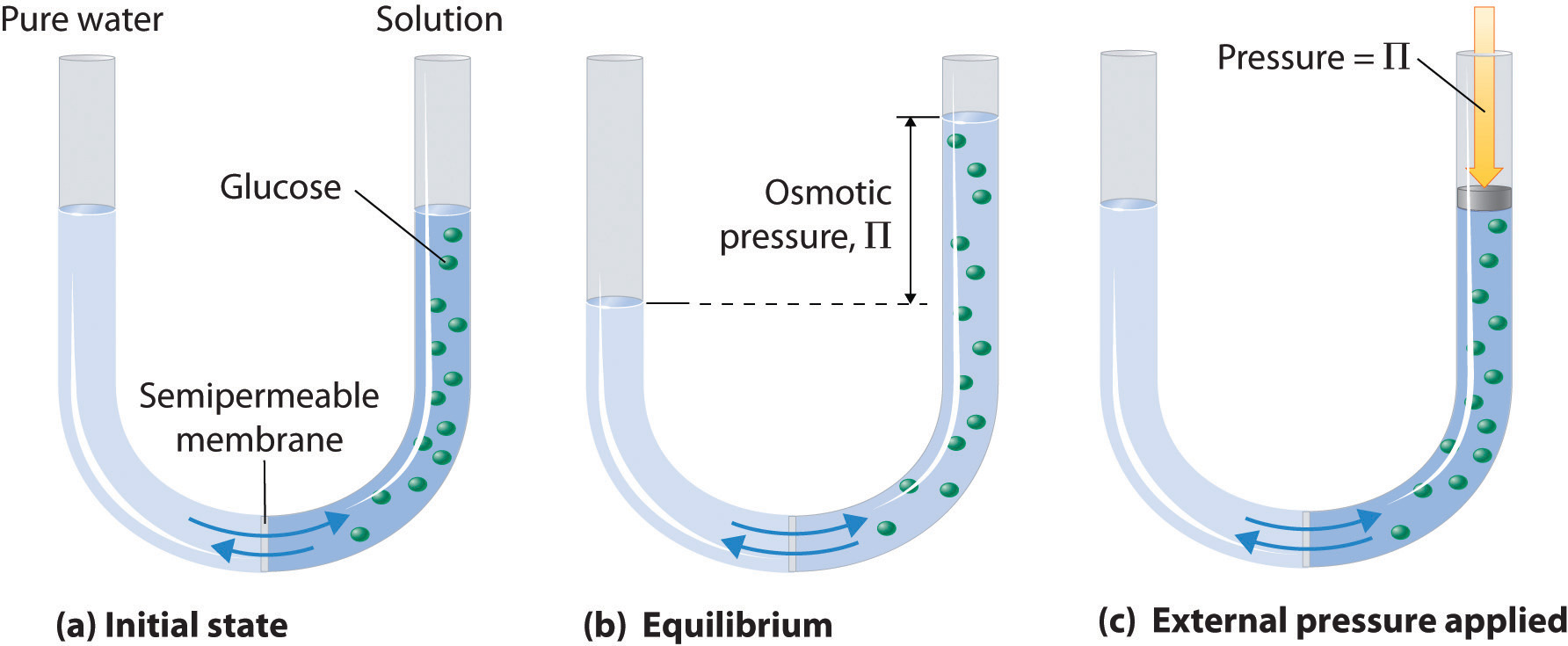
Osmotic pressure can be calculated using the formula
#color(blue)(|bar(ul(color(white)(a/a)Pi = i * c_"solute" * RTcolor(white)(a/a)|)))" "# , where
All you have to do here is rearrange this equation to solve for
Make sure to convert the temperature from degrees Celsius to Kelvin by using the conversion factor
#color(blue)(|bar(ul(color(white)(a/a)T["K"] = t[""^@"C"] + 273.15color(white)(a/a)|)))#
You will have
#c_"glucose" = Pi/(i * RT)#
#c_"glucose" = (7.7 color(red)(cancel(color(black)("atm"))))/(1 * 0.0821( color(red)(cancel(color(black)("atm"))) * "L")/("mol" * color(red)(cancel(color(black)("K")))) * (273.15 + 25) color(red)(cancel(color(black)("K"))))#
#c_"glucose" = "0.3146 mol L"^(-1)#
Rounded to two sig figs, the answer will be
#c_"glucose" = color(green)(|bar(ul(color(white)(a/a)"0.31 mol L"^(-1)color(white)(a/a)|)))#

