Question

The PERIMETER of isosceles trapezoid ABCD is equal to 80cm. The length of the line AB is 4 times bigger than lenght of a CD line which is 2/5 the lenght of the line BC (or the lines which are the same in lenght). What is the area of the trapezoid?

I'm sorry for the grammar mistakes etc.

Thanks!

Answer 1

Area of trapezium is `320` `cm^2`.

Explanation:

Let the trapezium be as shown below:

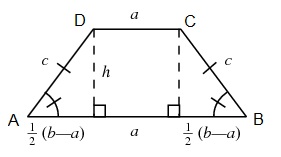
Here, if we assume smaller side `CD=a` and larger side `AB=4a` and `BC=a/(2/5)=(5a)/2`.

As such `BC=AD=(5a)/2`, `CD=a` and `AB=4a`

Hence perimeter is `(5a)/2xx2+a+4a=10a`

But perimeter is `80` `cm.`. Hence `a=8` cm. and two paallel sides shown as `a` and `b` are `8` cm. and `32` cm.

Now, we draw perpendiculars fron `C` and `D` to `AB`, which forms two identical right angled trianges, whose

hypotenuse is `5/2xx8=20` `cm.` and base is `(4xx8-8)/2=12`

and hence its height is `sqrt(20^2-12^2)=sqrt(400-144)=sqrt256=16`

and hence as area of trapezium is `1/2xxhxx(a+b)`, it is

`1/2xx16xx(32+8)=8xx40=320` `cm^2`.