Question

The `"pH"` at one-half the equivalence point in an acid-base titration was found to be `5.67`. What is the value of `K_a` for this unknown acid?

Answer 1

`K_a = 2.1 * 10^(-6)`

Explanation:

The idea here is that at the half equivalence point, the `"pH"` of the solution will be equal to the `"p"K_a` of the weak acid.

Assuming that you're titrating a weak monoprotic acid `"HA"` with a strong base that I'll represent as `"OH"^(-)`, you know that at the equivalence point, the strong base will completely neutralize the weak acid.

`"HA"_ ((aq)) + "OH"_ ((aq))^(-) -> "A"_ ((aq))^(-) + "H"_ 2"O"_ ((l))`

So when you're adding equal numbers of moles of weak acid and of strong base, all the moles of the weak will be consumed and you'll be left with `"A"^(-)`, the conjugate base of the weak acid.

Now, at the half equivalence point, you're adding enough moles of the strong base to neutralize half of the moles of the weak acid present in the solution.

The reaction will consume half of the moles of the weak acid and produce just as many moles of the conjugate base `->` the weak acid, the strong base, and the conjugate base are all in `1:1` mole ratios, meaning that what you consume from the weak acid and the strong base, you produce as the conjugate base.

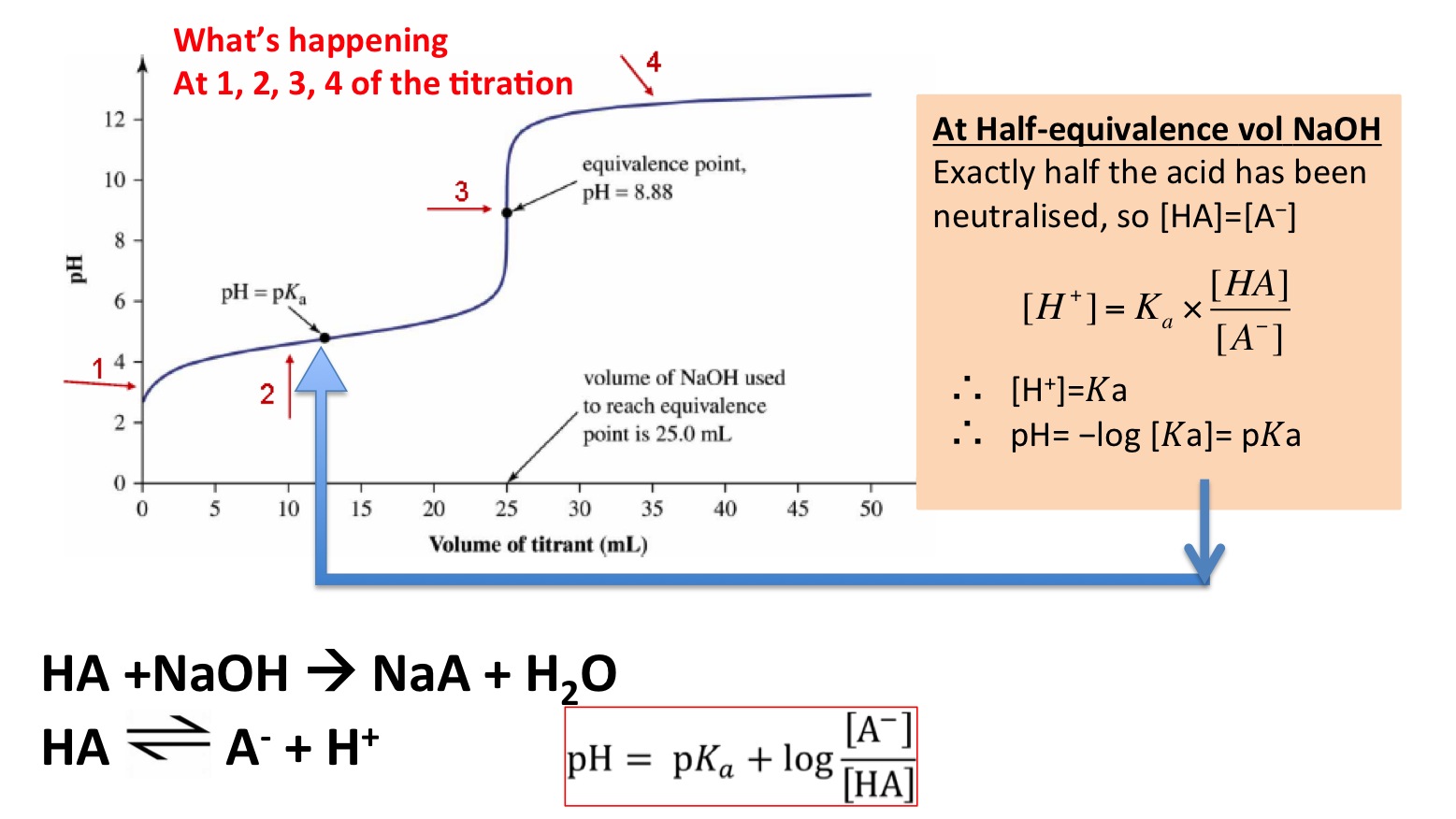
And so at the half equivalence point, the solution will contain equal numbers of moles of the weak acid and of its conjugate base, which implies that you're now dealing with a buffer solution.

As you know, the `"pH"` of a weak acid-conjugate base buffer can be calcualted using the Henderson - Hasselbalch equation

`"pH" = "p"K_a + log( (["conjugate base"])/(["weak acid"]))`

At the half equivalence point, you have

`["HA"] = ["A"^(-)]`

which implies that

`log( (["HA"])/(["A"^(-)])) = log(1) = 0`

Therefore, you can say that at the half-equivalence point, the `"pH"` of the solution is equal to the `"p"K_a` of the weak acid.

`color(blue)(ul(color(black)("At the half equivalence point: " -> " pH" = "p"K_a)))`

The `"p"K_a` is given by the acid dissociation constant of the weak acid, `K_a`.

`"p"K_a = - log(K_a)`

which implies that you have

`K_a = 10^(-"p"K_a)`

At the half equivalence point, you will have

`K_a = 10^(-"pH")`

Plug in your value to find

`K_a = 10^(-5.67) = color(darkgreen)(ul(color(black)(2.1 * 10^(-6))))`

The answer is rounded to two sig figs, the number of decimal places you have for the `"pH"` of the solution.