The potential energy of gravitational interaction of a point mass m and a thin uniform rod of mass M and length L ,if they are located along the straight line at a distance 'a' from each other?
1 Answer
Apr 22, 2017
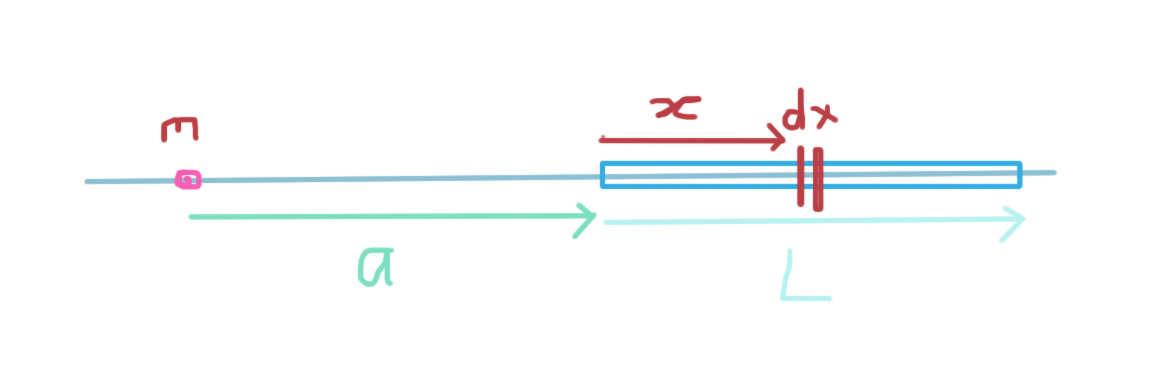
For this set up, we get the potential gravitational energy
-
small element of width
#dx# and mass#dM# ; and -
the mass m.
And
So
With a point mass assumption and the same set up:
They don't look that similar but if you play around with expansions or plot they do look alike.

