The rate of rotation of a solid disk with a radius of #8 m# and mass of #2 kg# constantly changes from #2 Hz# to #8 Hz#. If the change in rotational frequency occurs over #12 s#, what torque was applied to the disk?
1 Answer
Explanation:
Torque can be expressed by the following equation:
#color(darkblue)(tau=Ialpha)# where
#I# is the moment of inertia of the object and#alpha# is its angular acceleration
Since a specific
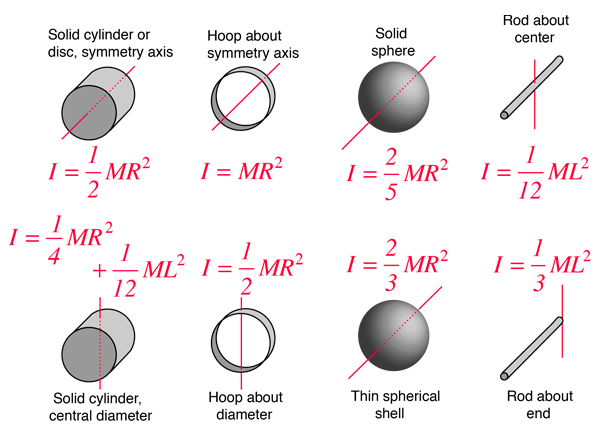
The average angular acceleration is given by:
#color(red)(alpha_(avg)=(Deltaomega)/(Deltat))# where
#omega# is the angular velocity of the disk and#Deltat# is the period over which the change occurs
Since
#color(red)(alpha_(avg)=(2pi(f_f-f_i))/(Deltat))#
Putting all of the above together, we have the equation:
#color(darkblue)(tau=1/2MR^2*(2pi(f_f-f_i))/(Deltat))#
We are given the following information:
#|->"M"=2"kg"# #|->"R"=8"m"# #|->"f"_i=2"s"^-1# #|->"f"_f=8"s"^-1# #|->Deltat=12"s"#
Substituting these values into the equation we derived above, we have:
#tau=1/2(2"kg")(8"m")^2*(2pi(8"s"^-1-2"s"^-1))/(12"s")#
#=201.062"Nm"#
#~~201"Nm"#
Note this occurs in the counterclockwise direction as the convention is that counterclockwise is positive.

