Question

The region bounded by the curve y=ln(x)/x and the lines x=1, x=e, y=0 is rotated around x=2π. Find the volume of the solid generated. How would I go about solving this? Doesn’t the integral need to be in terms of y, but ln(x)/x does not have a inverse.

Answer 1

See below

Explanation:

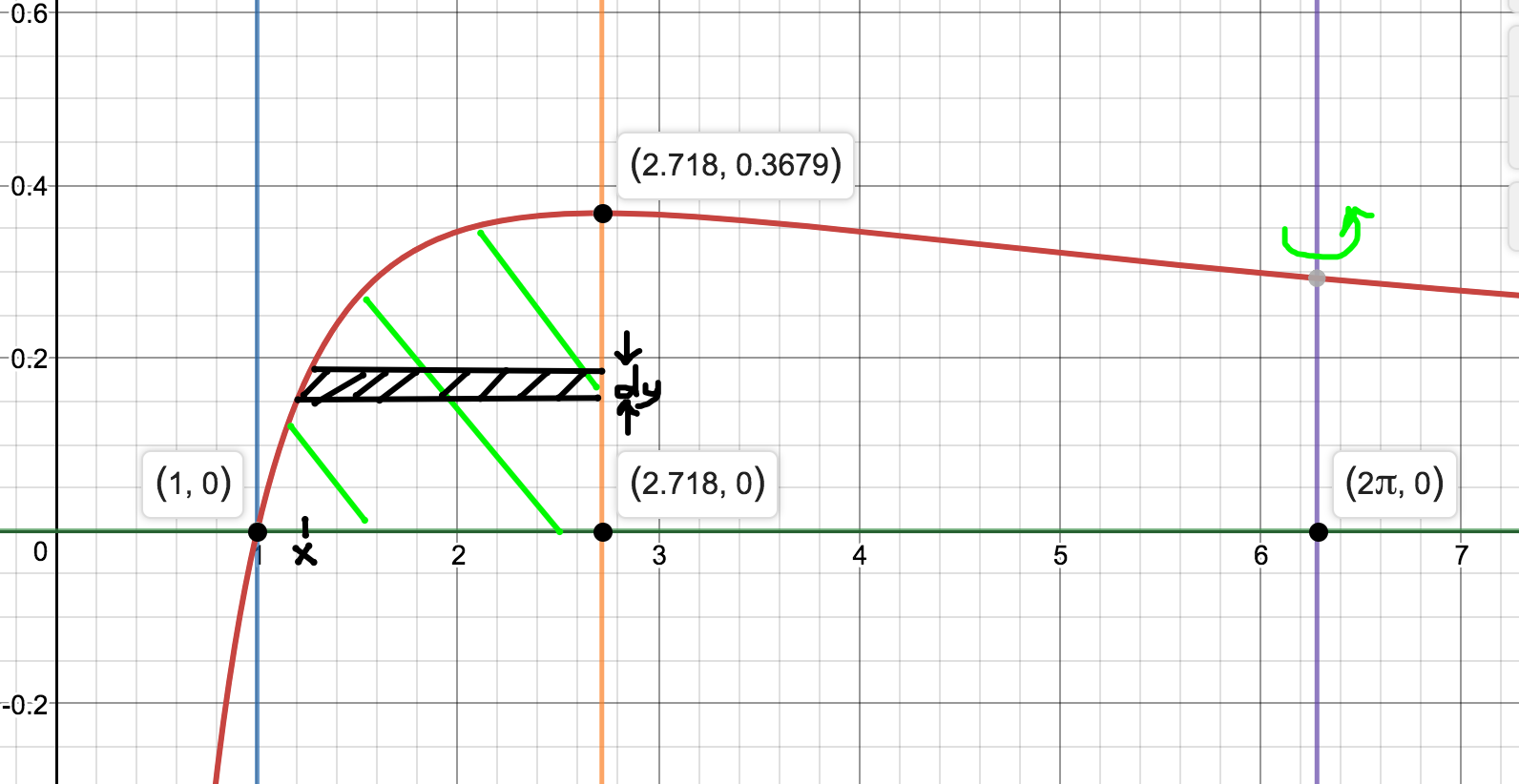
If you do it this way:

`dV = dy(pi( 2 pi - x)^2 - pi(2 pi - e)^2) = pi dy (x^2 - 4 pi x + e(4 pi - e))`

The integral is:

`V =pi int_(x=1)^e \ x^2 - 4 pi x + e(4 pi - e) \ dy`

`=pi int_(x=1)^e \ x^2 - 4 pi x + e(4 pi - e) \ d((ln x)/x)`

`=pi int_(x=1)^e \ (x^2 - 4 pi x + e(4 pi - e) )\ ((1 - ln x)/x^2) \ dx = 2 pi(pi -1)`

You don't need an inverse. That's a machine result. I'm not sure I fancy the slog of doing it by hand but it is very do-able.

If you do it this way:

`dV = 2 pi (2 pi - x) \ dx \ y`

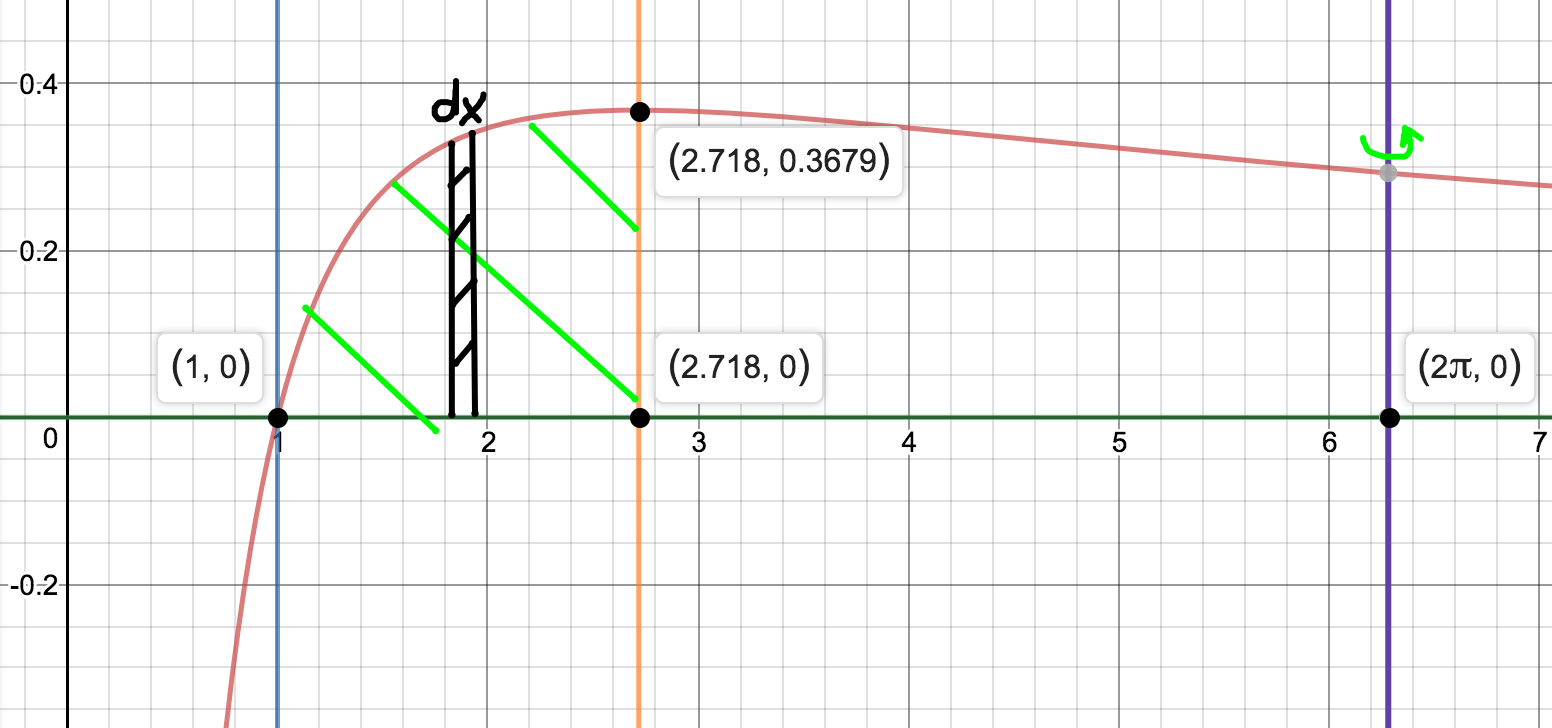
The integral is:

`V = 2 pi int_(x = 1)^e \ (2 pi - x) (ln x)/x \ dx`

`= 2 pi int_(x = 1)^e \ 2 pi (ln x)/x- ln x \ dx`

These results are trivial:

• `int \ dx \ (ln x)/x = (ln^2 x)/2 + C`

• `int \ dx \ ln x = x ln x - x + C`

`= 2 pi[ \ pi ln^2 x- x ln x + x ]_(x = 1)^e`

`= 2 pi (pi -1)`