Question

The region under the curves `y=sqrt(e^x+1), 0<=x<=3` is rotated about the x axis. How do you sketch the region and find the volumes of the two solids of revolution?

Answer 1

Please see below. (There is only one solid.)

Explanation:

To sketch `y = sqrt(e^x+1)` note that the `y` intercept is `sqrt(2) ~~ 1.4`.

And at `x=3`, we have `y= sqrt(e^3+1)` which is close to `4.5`.

Arithmetic approximation:
(`e~~2.7` so `e^3 ~~ 2.7^3`. now, `2.7 * 2.7 ~~7.3` and `2.7 * 7.3 ~~19.7`. So `e^3 +1` is near `21` and `4.5^2 = 20.25` since `(n+0.5)^2 = n(n+1) +0.25`.)

The derivative: `y' = e^x/(2sqrt(e^x+1))` is always positive, so the function is increasing.

(For a better sketch investigate concavity. The graph is concave up.)

The region is shaded blue.

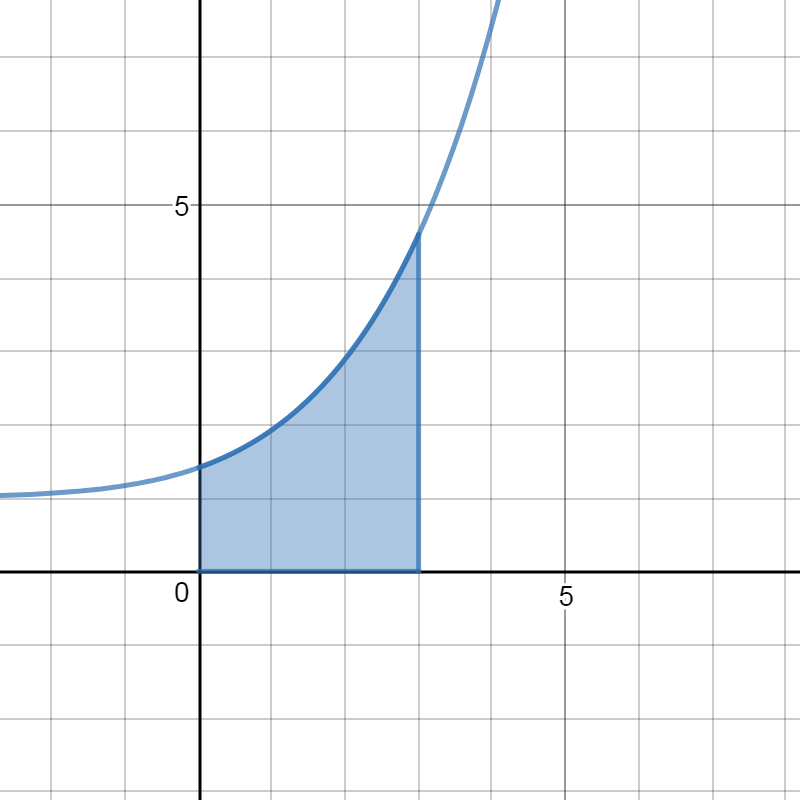
To go around the `x` axis, I used disks.

The volume of a representative disk is

`pi("radius")^2 xx "thickness" = pi(sqrt(e^x+1))^2 dx = pi(e^x+1) dx`

Since `x` varies from `0` to `3`, the volume of the solid is

`V = pi int_0^3(e^x+1) dx = pi[e^x+x]_0^3 = pi(e^3+2)`