Question

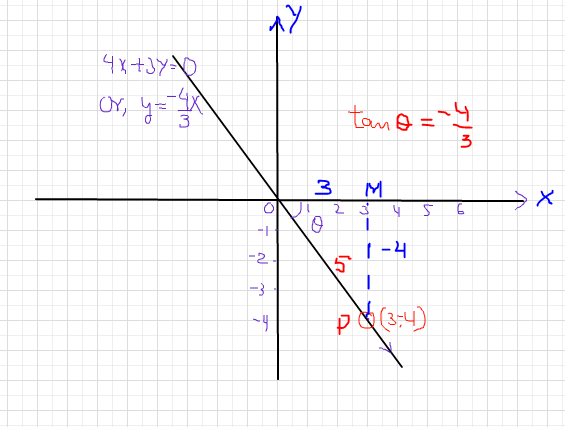
The terminal side of `theta` lies on the line `4x+3y=0` in quadrant IV, how do you find the values of the six trigonometric functions by finding a point on the line?

Answer 1

`sin theta= -4/5`; `cos theta= 3/5` ; `tan theta=-4/3` ; `sec theta =5/3`; `csc theta=-5/4` and `cot theta= -3/4`

Explanation:

The slope of the given line is `tan^ (-1) ( (-4)/3)` or `arc tan ((-4)/3)`. This means there is a point on this line with coordinates (3, -4). Its radial distance from the origin would be `sqrt(3^3 +4^2)` =5

The angle `theta` is, therefore, such that `tan theta= (-4)/3`.

As shown in the figure below, triangle OPM is a rt. triangle, its hypotenuse is 5 with base and altitude being 3 and -4 respectively. Accordingly,
`sin theta= -4/5`; `cos theta= 3/5` ; `tan theta=-4/3` ; `sec theta =5/3`; `csc theta=-5/4` and `cot theta= -3/4`