Question

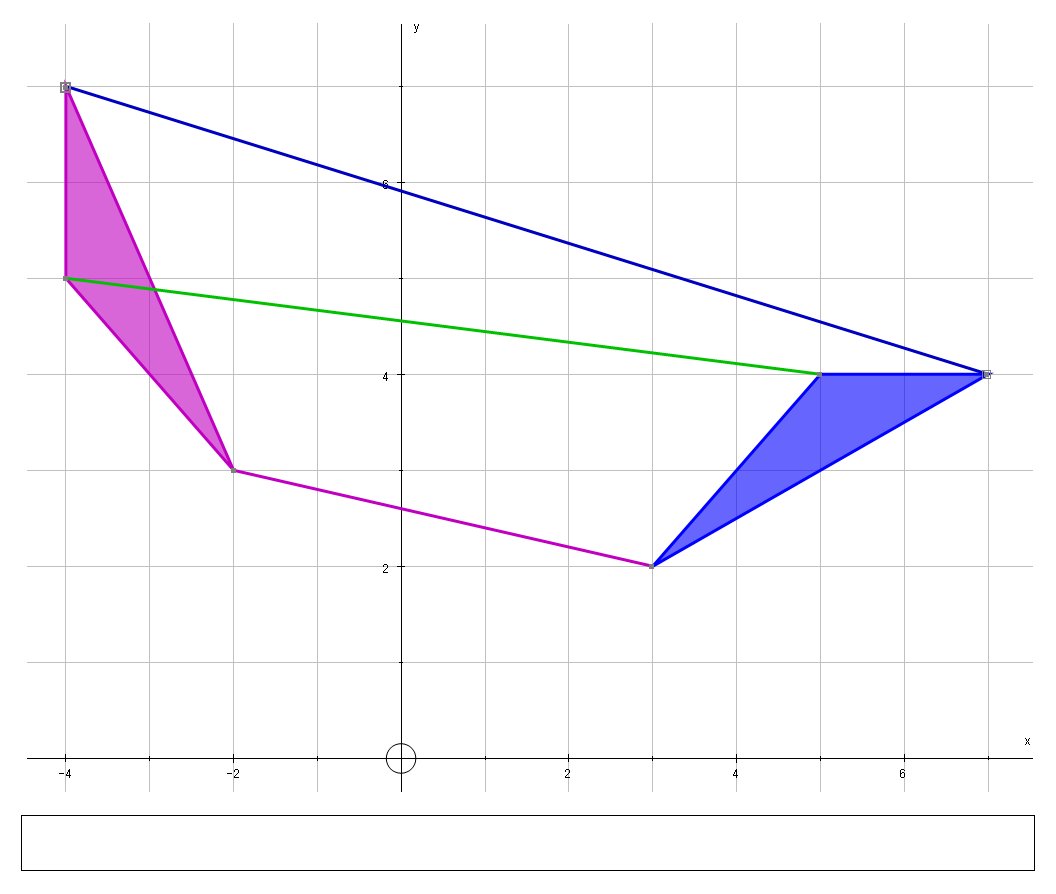
The triangle A with coordinates (3,2) (5,4) (7,4) can be mapped on to triangle D with a transformation matrix P. Find coordinates of D?

the transformation matrix for P is `(""^0 ""_(1) ""^(-1) ""_(0))`

Answer 1

`(-2,3)`, `(-4,5)` and `(-4,7)`

Explanation:

Triangle `A` is mapped to `D` via a Transformation matrix `bbP`, so given the column vector coordinates of `A`, `bb ul a`, `bb ul b` and `bb ul c`, say, we can write the destination coordinate as:

`bb ul (a)' = bb Pbb ul a`, `\ \ bb ul (b)' = bb P bb ul b`, and , `\ \ bb ul (c)' = bb Pbb ul c`,

Given the coordinates `(3,2)`, `(5,4)` and `(7,4)` and the matrix `bb P= ( (0,-1), (1,0))` we can write in matrix form as

`bb D = ( (0,-1), (1,0)) ( (3,5,7), (2,4,4) )`

`\ \ \ = ( (0*3-1*2, 0*5-1*4, 0*7-1*4), (1*3+0*2, 1*5+0*4, 1*7+0*4) )`

`\ \ \ = ( (-2, -4, -4), (3, 5, 7) )`

And so the respective coordinates of `D` are:

`(-2,3)`, `(-4,5)` and `(-4,7)`

And we can view the transformation graphically:

We can conclude that the matrix transformation represents an anti-clockwise rotation of `90^o` about the origin.