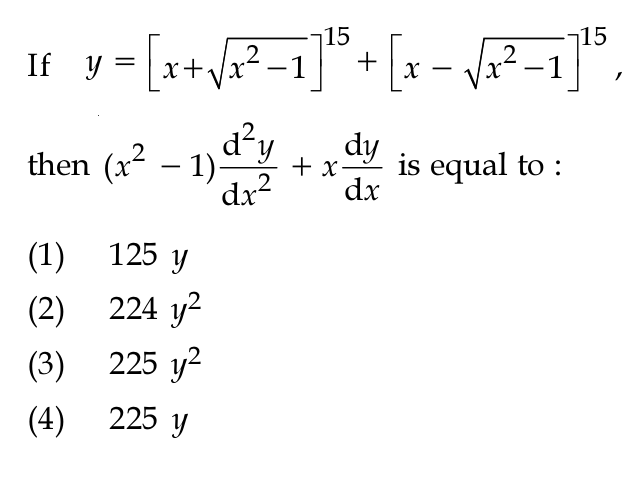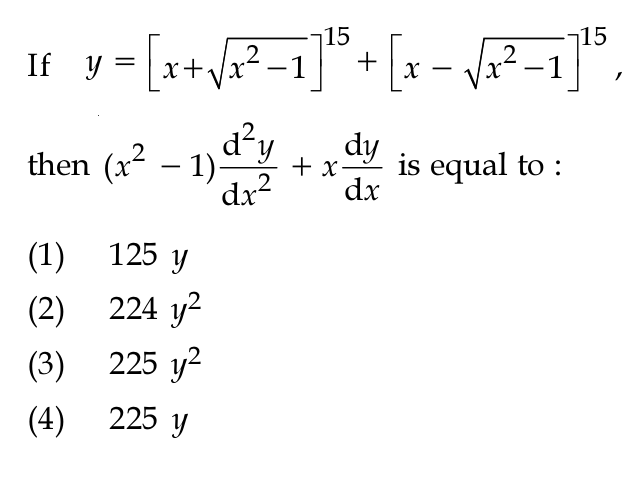#y=(x+sqrt(x^2-1))^15+(x-sqrt(x^2-1))^15#
Hence #(dy)/(dx)=15(x+sqrt(x^2-1))^14*(1+(2x)/(2sqrt(x^2-1)))+15(x-sqrt(x^2-1))^14*(1-(2x)/(2sqrt(x^2-1)))#
= #15(x+sqrt(x^2-1))^14*(1+x/sqrt(x^2-1))+15(x-sqrt(x^2-1))^14*(1-x/sqrt(x^2-1))#
= #15(x+sqrt(x^2-1))^14*((sqrt(x^2-1)+x)/sqrt(x^2-1))+15(x-sqrt(x^2-1))^14*((sqrt(x^2-1)-x)/sqrt(x^2-1))#
= #15(x+sqrt(x^2-1))^15/sqrt(x^2-1)-15(x-sqrt(x^2-1))^15/sqrt(x^2-1)#
or #sqrt(x^2-1)/15(dy)/(dx)=(x+sqrt(x^2-1))^15-(x-sqrt(x^2-1))^15#
and similarly we have
#sqrt(x^2-1)/15(d^2y)/(dx^2)+(dy)/(dx)*(2x)/(30sqrt(x^2-1))=15(x+sqrt(x^2-1))^15/sqrt(x^2-1)+15(x-sqrt(x^2-1))^15/sqrt(x^2-1)#
or #(x^2-1)/225(d^2y)/(dx^2)+(dy)/(dx)*x/225=(x+sqrt(x^2-1))^15+(x-sqrt(x^2-1))^15=y#
or #(x^2-1)(d^2y)/(dx^2)+x(dy)/(dx)=225y#
Hence answer is (4).
Additional Information #-# Observe that for #y=(x+sqrt(x^2-1))^n+(x-sqrt(x^2-1))^n#, #(x^2-1)(d^2y)/(dx^2)+x(dy)/(dx)# would be #n^2y#