The velocity of a sailing boat in favor of the current in a river is 18km/hr and against the current, it is 6km/hr.In which direction the boat is to be driven in order to reach the other side of the river and what will be the velocity of the boat?
1 Answer
Let
Given that the velocity of the sailing boat in favor of the current in a river is 18km/hr and against the current, it is 6km/hr.We can write
Adding (1) and (2) we get
Subtracting (2) from (2) we get
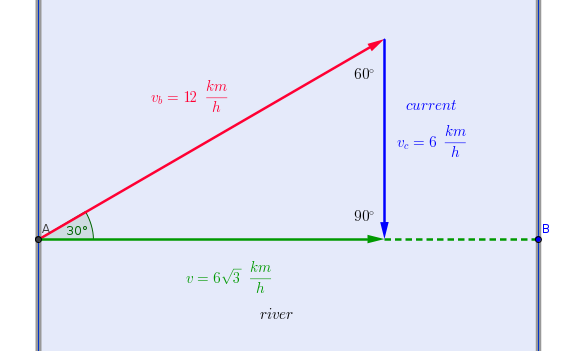
Now let us consider that
As the boat reaches just opposite point of the river, during sailing the resolved part of its velocity should balance the velocity of the current.Hence we can write
This angle is with the bank as well as with opposite direction of the current.
The other resolved part of the velocity of boat
So this velocity


