Question

Two charges of `3 C` and `-1 C` are positioned on a line at points `6` and `5`, respectively. What is the net force on a charge of `2 C` at `-2`?

Answer 1

`"Net force on charge 2C :"4.7*10^8N" ,at negative x direction."`

Explanation:

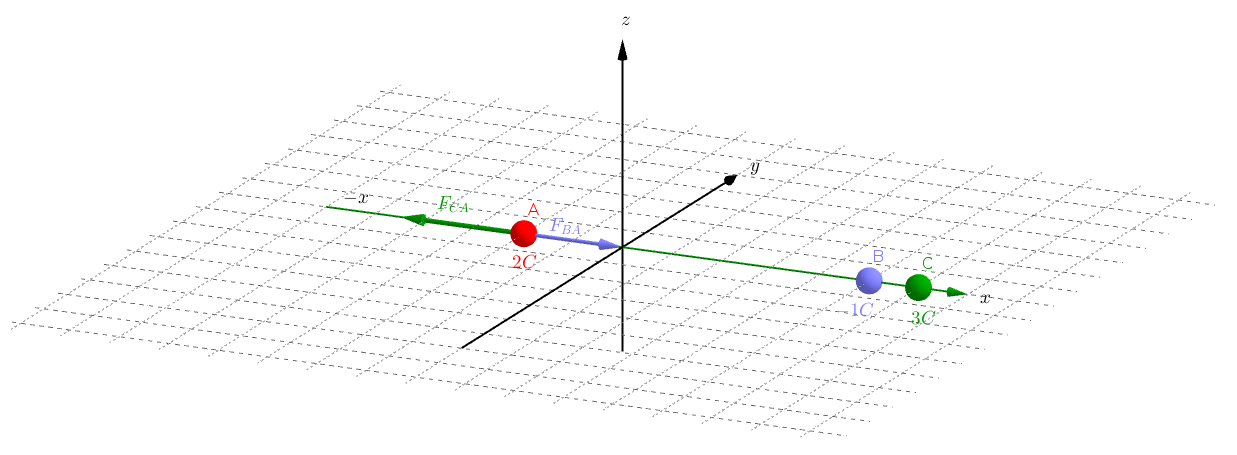
• The position of the point electric charges in the symbolic figure above is exaggerated.
• Coulomb's law states that electrical charges will force each other.
• It is a force pushing or pulling force between two charges.
• If the charges are the same, pushing is made, if it is reversed, pulling force occurs.
• We can calculate the force that the electric charges apply to each other by using the formula given below.

`F=K*(q_1*q_2)/d^2`
`"where ;"`
`q_1:"first charge"`
`q_2:"second charge"`
`d:"distance between "q_1" and "q_2`
`k:9.10^9 N*m^2*C^(-2)`

• Both the B and C spheres apply force to the A sphere.
• The net force applied to A is equal to the vector sum of the forces.
• Let's calculate the force that B applies to A.

`color(blue)(F_("BA")=K*(-1*2)/7^2=-(2K)/49)`

• Let's calculate the force that C applies to A.

`color(green)(F_("CA")=K*(3*2)/8^2=(6K)/64)`

• Now let's find the vector sum.

`Sigma F_("net")=color(blue)(F_("BA"))+color(green)(F_("CA"))`

`Sigma F_("net")=(-2K)/49+(6K)/64`

`Sigma F_("net")=(-128K+294K)/3136`

`Sigma F_("net")=(166K)/3136`

`Sigma F_("net")=(166*9*10^9)/3166`

`Sigma F_("net")=0.47*10^9`

`Sigma F_("net")=4.7*10^8N`

• The net force is in negative x direction.