Question

Two charges of `-6 C` and `-3 C` are positioned on a line at points `-5` and `8`, respectively. What is the net force on a charge of `4 C` at `2`?

Answer 1

The net force is `1.40xx10^9" N"` to the left.

Explanation:

The force between two charges is given by Coulomb's law:

`|vecF|=k(|q_1||q_2|)/r^2`

where `q_1` and `q_2` are the magnitudes of the charges, `r` is the distance between them, and `k` is a constant equal to `8.99xx10^9" Nm"^2//"C"^2`, sometimes referred to as Coulomb's constant.

• Since unspecified, I'll assume radii values to be in meters so that the units work out.

Here is a diagram of the situation:

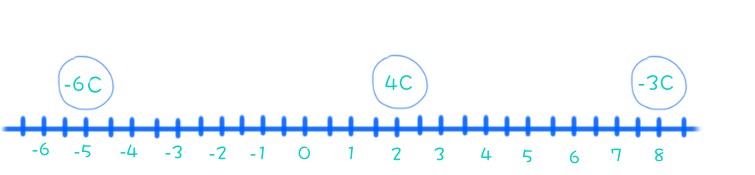
To find the net force on the `4C` charge, we consider the forces exerted on it by the `-6C` and `-3C` charges.

We have the following information:

• `|->Q_1=-6"C at " -5`
• `|->Q_2=4"C at " 2`
• `|->Q_3=-3"C at " 8`
• `|->k=8.99xx10^9" Nm"^2//"C"^2`

`color(blue)(vecF_("net on 3")=sumvecF=vecF_(1 on 2)+vecF_(3 on 2))`

Recall that like charges repel, while opposite charges attract. Each of the charges acting on `Q_2` are negative. Therefore, the force vectors can be drawn in as follows:

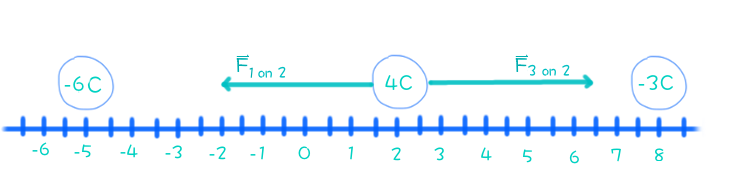
where `vecF_(1" on " 2)` is the force of `Q_1` on `Q_2` and `vecF_(3" on " 2)` is the force of `Q_3` on `Q_2`

So, we can calculate `vecF_(1" on " 2)` and subtract from the value we obtain from `vecF_(3" on " 2)` to find the net force on the `Q_2` charge.

`abs(vecF_(1" on " 2))=k*(|q_1||q_2|)/(r_(12)^2)`

`=(8.99xx10^9" Nm"^2//"C"^2)*(6C*4C)/(7"m")^2`

`color(blue)(=4.40xx10^(9)" N")`

`abs(vecF_(3" on " 2))=k*(|q_3||q_2|)/(r_(32)^2)`

`=(8.99xx10^9" Nm"^2//"C"^2)*(3C*4C)/(6)^2`

`color(blue)(=3.00xx10^9" N")`

Therefore, we have:

`color(blue)(vecF_(n e t)=-1.40xx10^9" N")`

That is, `1.40xx10^9" N"` to the left.

`- - - - - - - -`

Here is what the forces exerted on charges by other charges of the same or different sign look like: