Two charges of # -7 C # and # -4 C# are positioned on a line at points # -9 # and # 7 #, respectively. What is the net force on a charge of # 4 C# at # -2 #?
1 Answer
5.14x
Explanation:
The charges you have described are very large, so the Forces are also very large. Usually Coulombs are measured in micro (
or nano (
Since the charges are in line, we do not have to find the components of any of the vectors.
The questions is about Electric Fields. Every charge creates an electric field. The strength of the field is dependent on the magnitude of the charge. (In this case it is
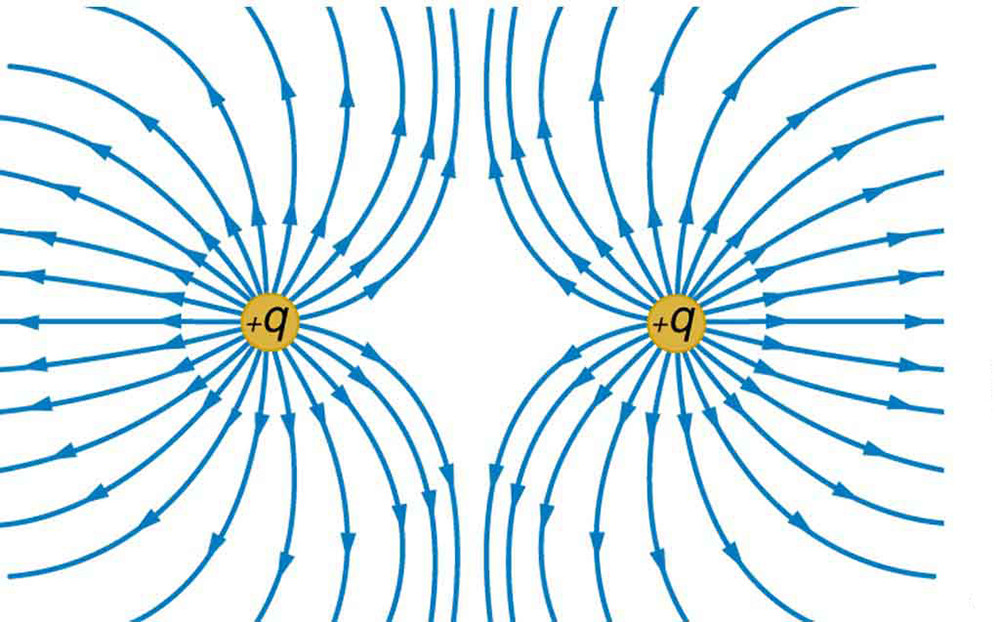
Similarly, the charges from the above question will repel each other, since they are both negative.
Here is the math.
You can calculate the strength of an electric field from the equation:
To calculate force of a charge, we use the equation
From here it is a matter of identifying your charges and calculating. For me:
The electric field of
Now that we have found the Electric Field of
Therefore the force of
Here is a good animation and activity: here This animation allow you to see how the force increses as charges are placed nearer or farther away from each other.

