Two circles are externally tangent. Common tangents to the circles form an angle of measure #2x#. How do you prove the ratio of the radii of the circles is #(1 - sinx)/(1+ sinx)#?

1 Answer
Shwetank Mauria
Dec 23, 2017

Please see below.

Explanation:

Let us have the two circles centered at #P# and #Q#, with radius #R_1# and #R_2# respectively.

Let the two tangents be #LMN# and #GHN#, where #L,M,G,H# are the points at which they touch the circles as shown and #N# is the point at which they intersect each other.

The line joining #PQ# will also pass through #N#. Now join points of contact of tangents #L,M,G,H# with the respective centers of the circles as shown. Let #m/_LNG=2x#, then #m/_LNP=x#.
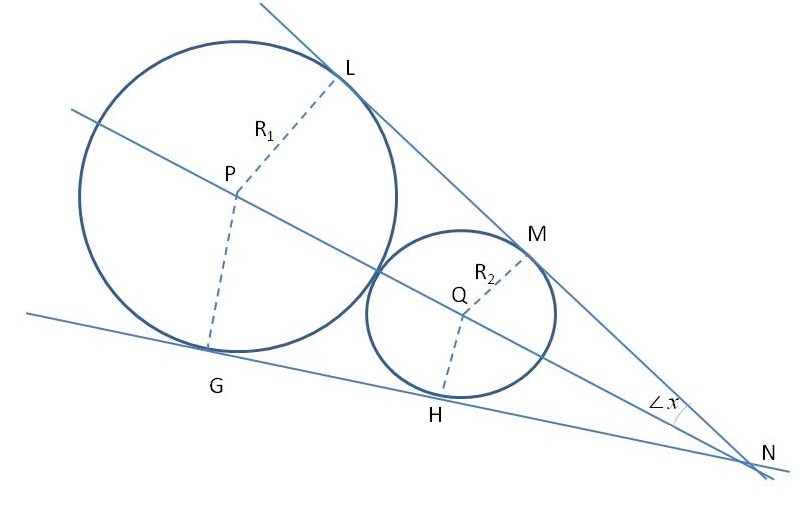
enter image source here
Now #DeltasLNP# and #MNQ# are right angles and hence

#R_1=PNsinx# .....................(A)

and #R_2=QNsinx# .....................(B)

Subtracting (B) from (A), we get

#R_1-R_2=(PN-QN)sinx#

or #sinx=(R_1-R_2)/(PQ)=(R_1-R_2)/(R_1+R_2)#

or #1/sinx=(R_1+R_2)/(R_1-R_2)#

Applying componendo and dividendo

#(1+sinx)/(1-sinx)=(R_1+R_2+R_1-R_2)/(R_1+R_2-R_1+R_2)#

#(1+sinx)/(1-sinx)=(2R_1)/(2R_2)#

or #R_2/R_1=(1-sinx)/(1+sinx)#

Related questions
Impact of this question
4693 views around the world
You can reuse this answer
Creative Commons License