Question

Two people meet in the purple room on the fourth floor of a building. On departure, one person travels West 16 feet, South 9 feet, and Down 9 feet. The other person travels North 16 feet, East 8 feet, and Up 9 feet. How far apart are the two people? Round

Answer 1

I get `"40.5 ft"`.

If you want me to round to the nearest integer, it would actually be about `"40 ft"`. Without rounding, it was `40.4598cdots` `"ft"`.

Interestingly enough, the distances each person walked were `(1)` `"20.45 ft"` and `(2)` `"20.02 ft"`, respectively, which add up to be just a LITTLE longer than the total distance between them. So, the angle between the two travel paths must be nearly `180^@`.

(In fact, it is `177.43^@`.)

---

Well, let's draw this out in 3D space to see what is asked for. I assume up/down refers to altitude (`z` axis). West is `-x` direction, north is `+y` direction, etc.

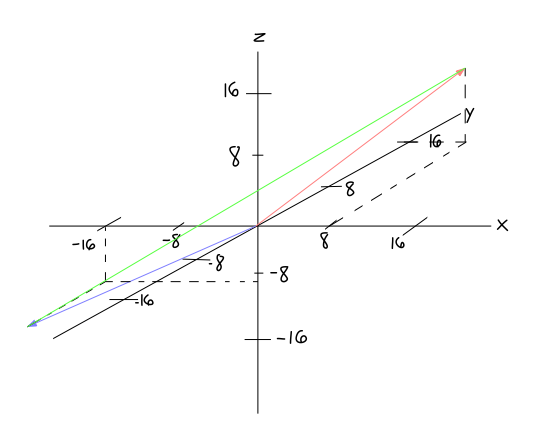
Suppose person `1` was the `color(blue)("blue")` arrow and person `2` was the `color(red)("red")` arrow. The distance between them is the `color(green)("green")` line.

The point that they land upon is a vector.

`color(blue)(vecv_1) = << -16, -9, -9 >>`

`color(red)(vecv_2) = << +16, +8, +9 >>`

Do not simply add the vectors together as they are:

`color(blue)(vecv_1) + color(red)(vecv_2) = << 0, -1, 0 >>`

What we actually need to do is reverse the vector `vecv_1` so that both point in the same direction. That way, the components don't cancel out in the `x` and `z` directions, and we do get a distance farther than `"1 ft"`, which would be physically NOT what is represented on the diagram.

Thus, what we should do is add `-vecv_1` instead:

`color(green)(vecv_3) = -color(blue)(vecv_1) + color(red)(vecv_2)`

`= - << -16, -9, -9 >> + << +16, +8, +9 >>`

`= << +16, +9, +9 >> + << +16, +8, +9 >>`

`= << +32, +17, +18 >>`

Lastly, we need to find the length of this vector to determine the distance:

`color(green)(|vecv_3|) = sqrt(x^2 + y^2 + z^2)`

`= sqrt(("32 ft")^2 + ("17 ft")^2 + ("18 ft")^2)`

`=` `color(green)("40.5 ft")`