Calculate #E_(cell)# for a battery based in the following two half-reactions and conditions?
#"Cu (s)"\toCu^(2+)"(0.010 M)"+2e^-#
#MnO_4^(-)"(2.0 M)"+4H^+"(1.0 M)"+3e^(-)\toMnO_2"(s)"+2H_2O"(l)"#
I actually have everything... except #E_(cell)^o# , because I was not given voltages.
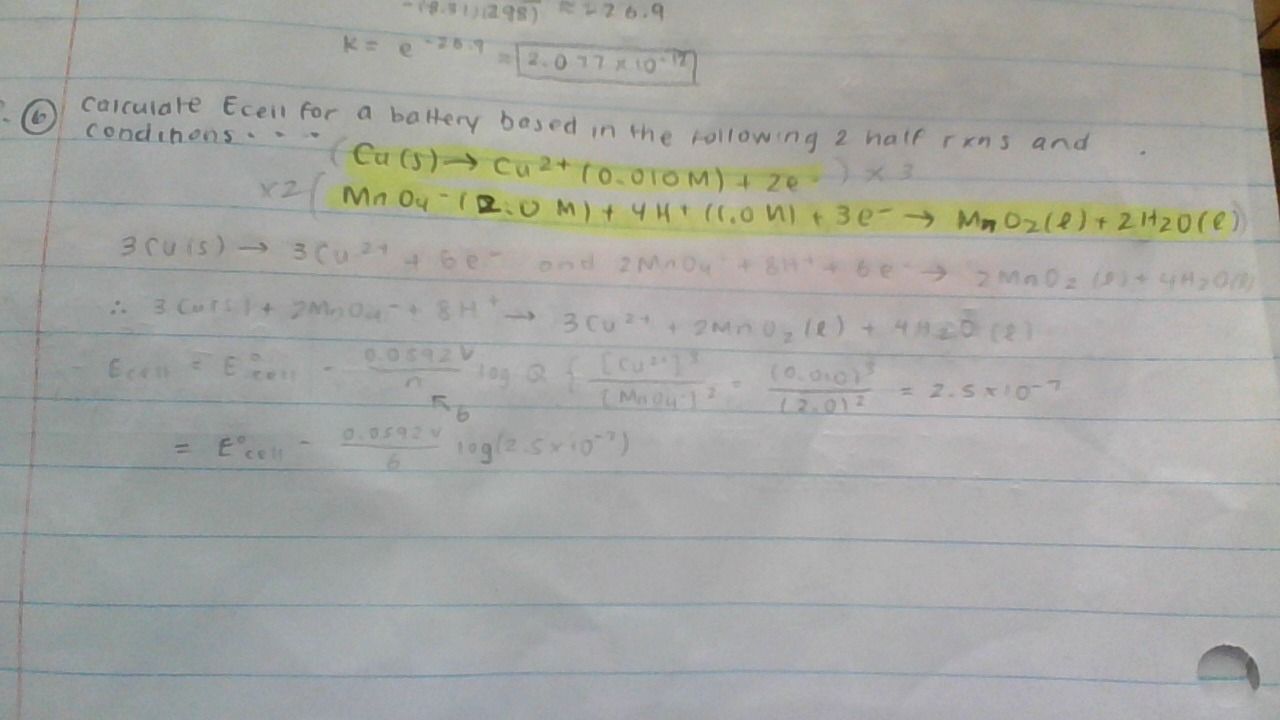
I actually have everything... except
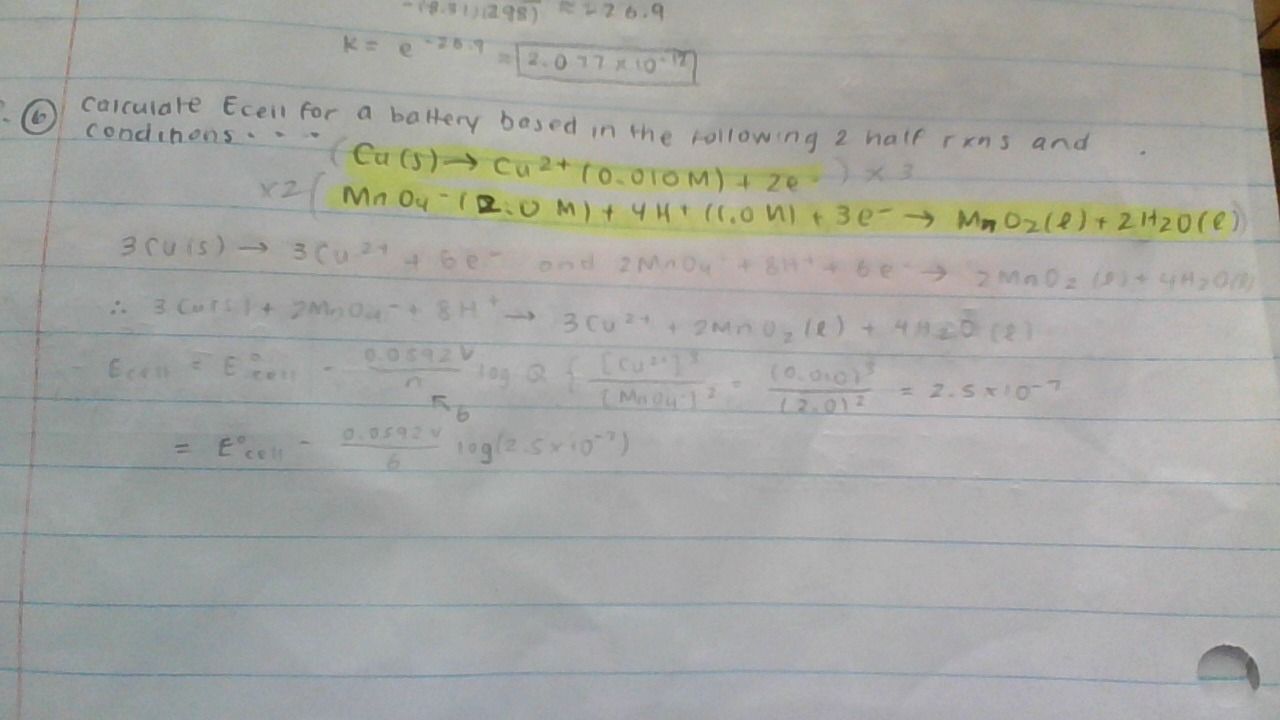
1 Answer
You should be given them, or you can look them up. I found them to be:
So, I get
The values are:
#3("Cu"(s) -> "Cu"^(2+)(aq) + cancel(2e^(-)))# ,#E_(red)^@ = "0.34 V"#
#ul(2("MnO"_4^(-)(aq) + 4"H"^(+)(aq) + cancel(3e^(-)) -> "MnO"_2(s) + 2"H"_2"O"(l)))# ,#E_(red)^@ = "1.67 V"#
#3"Cu"(s) + 2"MnO"_4^(-)(aq) + 8"H"^(+)(aq) -> 3"Cu"^(2+)(aq) + 2"MnO"_2(s) + 4"H"_2"O"(l)#
Hence, we can calculate
#E_(cell)^@#
#= {(overbrace(E_(red)^@)^"Reduction" + overbrace(E_(o x)^@)^"Oxidation"),(underbrace(E_"cathode"^@)_"Reduction" - underbrace(E_"anode"^@)_"Reduction"):}#
#= {("1.67 V" + (-"0.34 V")),("1.67 V" - "0.34 V"):}#
#= +"1.33 V"#
As a result, one can then calculate
#E_(cell) = E_(cell)^@ - (RT)/(nF)lnQ# where:
#R# and#T# are known from the ideal gas law as the universal gas constant#"8.134 V"cdot"C/mol"cdot"K"# and temperature in#"K"# .#n# is the total mols of electrons per mol of the atoms involved. Just take its value to be the number of electrons cancelled out from the balanced reaction.#F = "96485 C/mol e"^(-)# is Faraday's constant.#Q# is the reaction quotient, i.e. the not-yet equilibrium constant.
#Q = ((["Cu"^(2+)]//c^@)^3)/((["MnO"_4^(-)]//c^@)^2(["H"^(+)]//c^@)^8)#
#= ("0.010 M"//"1 M")^3/(("2.0 M"//"1 M")^2("1.0 M"//"1 M")^8)#
#= 2.5 xx 10^(-7)#
From here, assuming you mean
#color(blue)(E_(cell)) = "1.33 V" - ("8.314 V"cdotcancel"C"//cancel"mol"cdotcancel"K" cdot 298.15 cancel"K")/(((6 cancel("mol e"^(-)))/cancel"1 mol atoms") cdot 96485 cancel"C"//cancel("mol e"^(-)))ln(2.5 xx 10^(-7))#
#= "1.33 V" - ("0.0257 V")/(6)ln(2.5 xx 10^(-7))#
#= "1.33 V" - ("0.0592 V")/(6)log(2.5 xx 10^(-7))#
#= 1.39_5# #"V"#
#=># #color(blue)("1.40 V")#

